Question

10．已知雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1，（a＞0，b＞0）$的左右焦點分別為F₁，F₂，過右焦點F₂的直線交雙曲線于A，B兩點，連接AF₁，BF₁．若|AB|=|BF₁|，且∠ABF₁=90°，則雙曲線的離心率為$\sqrt{5-2\sqrt{2}}$．

Answer 1

分析 設|BF₁|=n，由題意可得|AB|=n，|AF₁|=$\sqrt{2}$n，運用雙曲線的定義和勾股定理，化簡整理，由離心率公式計算即可得到所求值．

解答 解：設|BF₁|=n，由|AB|=|BF₁|，且∠ABF₁=90°，可得
|AB|=n，|AF₁|=$\sqrt{2}$n，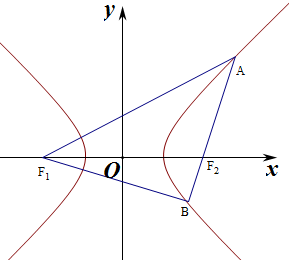
由雙曲線的定義可得|BF₁|-|BF₂|=2a，
即有|BF₂|=n-2a，
又|AF₁|-|AF₂|=2a，可得|AF₂|=$\sqrt{2}$n-2a，
由|AB|=（$\sqrt{2}$+1）n-4a=n，
解得n=2$\sqrt{2}$a，
在△F₁F₂B中，由|BF₁|²+|BF₂|²=|F₁F₂|²，
即為（2$\sqrt{2}$a）²+（2$\sqrt{2}$-2）²a²=4c²，
化為c²=（5-2$\sqrt{2}$）a²，
可得e=$\frac{c}{a}$=$\sqrt{5-2\sqrt{2}}$，
故答案為：$\sqrt{5-2\sqrt{2}}$，

點評 本題考查雙曲線的離心率的求法，運用雙曲線的定義和勾股定理是解決本題的關鍵，考查化簡整理的運算能力，屬于中檔題．