
【題目】已知f(x)=﹣3x2+a(6﹣a)x+b,a,b為實數.
(1)當b=﹣6時,解關于a的不等式f(1)>0;
(2)若不等式f(x)>0的解集為(﹣1,3),求實數a,b的值.
【答案】
(1)解:∵f(x)=﹣3x2+a(6﹣a)x+b,
∴b=﹣6時,f(1)=﹣3+a(6﹣a)+b=﹣a2+6a﹣9,
∴不等式f(1)>0可化為a2﹣6a+9<0,
即(a﹣3)2<0,
此不等式在實數范圍內無解,
即關于a的不等式f(1)>0的解集為
(2)解:∵f(x)=﹣3x2+a(6﹣a)x+b>0的解集為(﹣1,3),
∴方程﹣3x2+a(6﹣a)x+b=0的實數根為﹣1和3,
由根與系數的關系,得 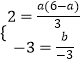 ,
,
解得a=3± ![]() ,b=9
,b=9
【解析】(1)計算f(1)的值,求b=﹣6時,關于a的不等式f(1)>0的解集即可;(2)根據一元二次不等式與對應一元二次方程之間的關系,利用根與系數的關系,即可求出a、b的值.
【考點精析】解答此題的關鍵在于理解解一元二次不等式的相關知識,掌握求一元二次不等式![]()
![]() 解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊.
解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2lnx,h(x)=x2﹣x+a.
(1)其求函數f(x)的極值;
(2)設函數k(x)=f(x)﹣h(x),若函數k(x)在[1,3]上恰有兩個不同零點求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我市九龍江南岸江濱路建設的持續推進,未來市民將新增又一休閑好去處,據悉南江濱路建設工程規劃配套建造一個長方形公園ABCD,如圖所示,公園由長方形的休閑區A1B1C1D1(陰影部分)和環公園人行道組成,已知休閑區A1B1C1D1的面積為4000m2 , 人行道的寬度分別為4m和10m.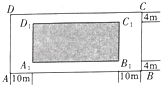
(1)若休閑區的長A1B1=x m,求公園ABCD所占面積S關于x的函數S(x)的解析式;
(2)要使公園所占面積最小,休閑區A1B1C1D1的長和寬該如何設計?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某職稱晉級評定機構對參加某次專業技術考試的100人的成績進行了統計,繪制了頻率分布直方圖(如圖所示),規定80分及以上者晉級成功,否則晉級失敗(滿分為100分).


(1)求圖中![]() 的值;
的值;
(2)估計該次考試的平均分![]() (同一組中的數據用該組的區間中點值代表);
(同一組中的數據用該組的區間中點值代表);
(3)根據已知條件完成下面![]() 列聯表,并判斷能否有85%的把握認為“晉級成功”與性別有關?
列聯表,并判斷能否有85%的把握認為“晉級成功”與性別有關?
(參考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sin ωxcos ωx-sin2ωx+1(ω>0)圖象的相鄰兩條對稱軸之間的距離為
sin ωxcos ωx-sin2ωx+1(ω>0)圖象的相鄰兩條對稱軸之間的距離為![]() .
.
(Ⅰ)求ω的值及函數f(x)的單調遞減區間;
(Ⅱ)如圖,在銳角三角形ABC中有f(B)=1,若在線段BC上存在一點D使得AD=2,且AC=![]() ,CD=
,CD=![]() -1,求三角形ABC的面積.
-1,求三角形ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線 ![]() (t為參數),
(t為參數), ![]() (
( ![]() 為參數).
為參數).
(1)化 ![]() ,
, ![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)過曲線 ![]() 的左頂點且傾斜角為
的左頂點且傾斜角為 ![]() 的直線
的直線 ![]() 交曲線
交曲線 ![]() 于
于 ![]() 兩點,求
兩點,求 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線 ![]() :
: 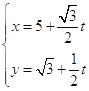 (t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的坐標方程為
(t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的坐標方程為 ![]() .
.
(1)將曲線C的極坐標方程化為直坐標方程;
(2)設點M的直角坐標為 ![]() ,直線l與曲線C的交點為A,B,求|MA||MB|的值.
,直線l與曲線C的交點為A,B,求|MA||MB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com