
【題目】在某地區2008年至2014年中,每年的居民人均純收入y(單位:千元)的數據如下表:
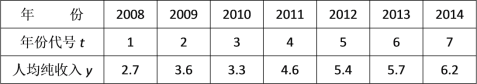
對變量t與y進行相關性檢驗,得知t與y之間具有線性相關關系.
(1)求y關于t的線性回歸方程;
(2)預測該地區2016年的居民人均純收入.
附:回歸直線的斜率和截距的最小二乘估計公式分別為:
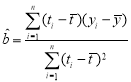 ,
,![]()
 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,過
,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(1)求![]() 的周長;
的周長;
(2)設點![]() 為橢圓
為橢圓![]() 的上頂點,點
的上頂點,點![]() 在第一象限,點
在第一象限,點![]() 在線段
在線段![]() 上.若
上.若![]() ,求點
,求點![]() 的橫坐標;
的橫坐標;
(3)設直線![]() 不平行于坐標軸,點
不平行于坐標軸,點![]() 為點
為點![]() 關于
關于![]() 軸的對稱點,直線
軸的對稱點,直線![]() 與
與![]() 軸交于點
軸交于點![]() .求
.求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 作與
作與![]() 軸不重合的直線
軸不重合的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,連接
兩點,連接![]() ,
,![]() 分別交直線
分別交直線![]() 于,
于,![]() ,
,![]() 兩點,若直線
兩點,若直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,試問:
,試問:![]() 是否為定值?若是,求出該定值,若不是,請說明理由.
是否為定值?若是,求出該定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是棱長為2的正方體,
是棱長為2的正方體,![]() 為面對角線
為面對角線![]() 上的動點(不包括端點),
上的動點(不包括端點),![]() 平面
平面![]() 交
交![]() 于點
于點![]() ,
,![]() 于
于![]() .
.

(1)試用反證法證明直線![]() 與
與![]() 是異面直線;
是異面直線;
(2)設![]() ,將
,將![]() 長表示為
長表示為![]() 的函數
的函數![]() ,并求此函數的值域;
,并求此函數的值域;
(3)當![]() 最小時,求異面直線
最小時,求異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 上橫坐標為4的點到焦點的距離為5.
上橫坐標為4的點到焦點的距離為5.

(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 與拋物線
與拋物線![]() 交于兩點
交于兩點![]() 、
、![]() ,且
,且![]() ,
,![]() 是弦
是弦![]() 中點,過
中點,過![]() 作平行于
作平行于![]() 軸的直線交拋物線
軸的直線交拋物線![]() 于點
于點![]() ,得到
,得到![]() ,再分別過弦
,再分別過弦![]() 、
、![]() 的中點作平行于
的中點作平行于![]() 軸的直線依次交拋物線
軸的直線依次交拋物線![]() 于點
于點![]() 、
、![]() ,得到
,得到![]() 和
和![]() ,按此方法繼續下去,解決下列問題:
,按此方法繼續下去,解決下列問題:
①求證:![]() ;
;
②計算![]() 的面積
的面積![]() ;
;
③根據![]() 的面積
的面積![]() 的計算結果,寫出
的計算結果,寫出![]() 、
、![]() 的面積,請設計一種求拋物線
的面積,請設計一種求拋物線![]() 與線段
與線段![]() 所圍成封閉圖形面積的方法,并求此封閉圖形的面積.
所圍成封閉圖形面積的方法,并求此封閉圖形的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三位同學畢業后,發現市內一些小家電配件的批發商每天的批發零售的生意很火爆,于是他們三人決定利用所學專業進行自主創業,專門生產這類小家電配件,并與經銷商簽訂了經銷合同,他們生產出的小家電配件,以每件![]() 元的價格全部由經銷商包銷.經市場調研,生產這類配件,每月需要投入固定成本為
元的價格全部由經銷商包銷.經市場調研,生產這類配件,每月需要投入固定成本為![]() 萬元,每生產
萬元,每生產![]() 萬件配件,還需再投入資金
萬件配件,還需再投入資金![]() 萬元.在月產量不足
萬元.在月產量不足![]() 萬件時,
萬件時,![]() (萬元);在月產量不小于
(萬元);在月產量不小于![]() 萬件時,
萬件時,![]() (萬元).已知月產量是
(萬元).已知月產量是![]() 萬件時,需要再投入的資金是
萬件時,需要再投入的資金是![]() 萬元.
萬元.
(1)試將生產這些小家電的月利潤![]() (萬元)表示成月產量
(萬元)表示成月產量![]() (萬件)的函數;(注:月利潤
(萬件)的函數;(注:月利潤![]() 月銷售收入
月銷售收入![]() 固定成本
固定成本![]() 再投入成本)
再投入成本)
(2)月產量為多少萬件時,這三位同學生產這些配件獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動點
中,動點![]() 到點
到點![]() 的距離和它到直線
的距離和它到直線![]() 的距離相等,記點
的距離相等,記點![]() 的軌跡為
的軌跡為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設點![]() 在曲線
在曲線![]() 上,
上,![]() 軸上一點
軸上一點![]() (在點
(在點![]() 右側)滿足
右側)滿足![]() ,若平行于
,若平行于![]() 的直線與曲線
的直線與曲線![]() 相切于點
相切于點![]() ,試判斷直線
,試判斷直線![]() 是否過點
是否過點![]() ?并說明理由.
?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據《人民網》報道,“美國國家航空航天局(NASA)發文稱,相比20年前世界變得更綠色了,衛星資料顯示中國和印度的行動主導了地球變綠.”據統計,中國新增綠化面積的420/0來自于植樹造林,下表是中國十個地區在2017年植樹造林的相關數據.(造林總面積為人工造林、飛播造林、新封山育林、退化林修復、人工更新的面積之和)單位:公頃
按造林方式分 | ||||||
地區 | 造林總面積 | 人工造林 | 飛播造林 | 新封山育林 | 退化林修復 | 人工更新 |
內蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重慶 | 226333 | 100600 | 62400 | 63333 | ||
陜西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肅 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
寧夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(Ⅰ)請根據上述數據,分別寫出在這十個地區中人工造林面積與造林總面積的比值最大和最小的地區;
(Ⅱ)在這十個地區中,任選一個地區,求該地區人工造林面積與造林總面積的比值不足50%的概率是多少?
(Ⅲ)從上表新封山育林面積超過十萬公頃的地區中,任選兩個地區,求至少有一個地區退化林修復面積超過五萬公頃的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com