
 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | $\frac{2015}{672}$ | D. | $\frac{2015}{336}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
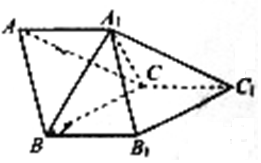 如圖所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,則下列結論正確的是( )
如圖所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,則下列結論正確的是( )| A. | :當AA1=$\frac{\sqrt{42}}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{3\sqrt{7}}{7}$ | |
| B. | :當AA1=$\frac{6}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{3\sqrt{7}}{7}$ | |
| C. | :當AA1=$\frac{\sqrt{42}}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{6}{7}$$\sqrt{7}$ | |
| D. | :當AA1=$\frac{6}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{6}{7}$$\sqrt{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com