
分析 (1)由題意列關于a,b,c的方程組,求解方程組可得a,b的值,則橢圓方程可求;
(2)聯立直線方程和橢圓方程,化為關于x的一元二次方程,由判別式大于0求得m的范圍,再由根與系數的關系結合$\overrightarrow{AO}•\overrightarrow{BO}<0$進一步求得m的范圍得答案.
解答 解:(1)由題意,$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1,c=1.
∴橢圓C的方程為:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)聯立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0.
由△=16m2-12(2m2-2)>0,得m2<3.
設A(x1,y1),B(x2,y2),
則${x}_{1}+{x}_{2}=-\frac{4m}{3},{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{3}$,①
∵∠AOB為鈍角,∴$\overrightarrow{AO}•\overrightarrow{BO}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}<0$,
即$2{x}_{1}{x}_{2}+m({x}_{1}+{x}_{2})+{m}^{2}<0$,②
把①代入②得:$2×\frac{2{m}^{2}-2}{3}-\frac{4}{3}m×m+{m}^{2}<0$,
解得:$-\frac{2\sqrt{3}}{3}<m<\frac{2\sqrt{3}}{3}$.
∵A、B、O三點不共線,∴m≠0.
∴實數m的取值范圍為($-\frac{2\sqrt{3}}{3},0$)∪(0,$\frac{2\sqrt{3}}{3}$).
點評 本題考查橢圓的簡單性質,考查橢圓標準方程的求法,訓練了平面向量在求解圓錐曲線問題中的應用,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±3) | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±5) | ||
| C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±3) | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±5) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
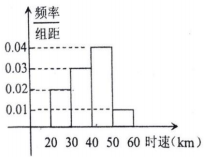 太原市某時段100輛汽車通過祥云橋時,時速的頻率分布直方圖如圖所示,則時速在[30,40]的汽車約有( )
太原市某時段100輛汽車通過祥云橋時,時速的頻率分布直方圖如圖所示,則時速在[30,40]的汽車約有( )| A. | 30輛 | B. | 35輛 | C. | 40輛 | D. | 50輛 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{15}{4}$ | B. | $\frac{13}{4}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com