
【題目】對于函數![]() ,若存在實數
,若存在實數![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 的不動點.
的不動點.
(1)當![]() ,
,![]() 時,求
時,求![]() 的不動點;
的不動點;
(2)若對于任何實數![]() ,函數
,函數![]() 恒有兩相異的不動點,求實數
恒有兩相異的不動點,求實數![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若![]() 的圖象上
的圖象上![]() 、
、![]() 兩點的橫坐標是函數
兩點的橫坐標是函數![]() 的不動點,且直線
的不動點,且直線![]() 是線段
是線段![]() 的垂直平分線,求實數
的垂直平分線,求實數![]() 的最小值.
的最小值.
【答案】(1)不動點是-1,2.(2)![]() (3)
(3)![]()
【解析】
(1)根據不動點定義,代入![]() ,
,![]() ,即可得一元二次方程,解方程即可求解.
,即可得一元二次方程,解方程即可求解.
(2)令![]() ,可得一元二次方程.根據有兩個相異的實數根,可知對應判別式
,可得一元二次方程.根據有兩個相異的實數根,可知對應判別式![]() .即可得關于
.即可得關于![]() 的不等式.再由對于任意實數
的不等式.再由對于任意實數![]() 恒成立,可知對應判別式
恒成立,可知對應判別式![]() 即可求得
即可求得![]() 的取值范圍;
的取值范圍;
(3)根據題意可設![]() ,
,![]() ,即可求得直線
,即可求得直線![]() 的斜率.根據直線
的斜率.根據直線![]() 是線段
是線段![]() 的垂直平分線,可求得
的垂直平分線,可求得![]() 的值.設
的值.設![]() 的中點為
的中點為![]() ,由韋達定理可得
,由韋達定理可得![]() ,代入直線
,代入直線![]() 即可用
即可用![]() 表示出
表示出![]() .結合基本不等式即可求得
.結合基本不等式即可求得![]() 的取值范圍,即可得
的取值范圍,即可得![]() 的最小值.
的最小值.
∵![]()
(1)當![]() ,
,![]() 時,
時,![]()
設![]() 為其不動點,即
為其不動點,即![]() .
.
則![]() .
.
∴![]() ,
,![]() .
.
即![]() 的不動點是-1,2.
的不動點是-1,2.
(2)由![]() 得
得![]() .由已知,此方程有相異二實根,
.由已知,此方程有相異二實根,
![]() 恒成立,即
恒成立,即![]() .
.
即![]() 對任意
對任意![]() 恒成立.
恒成立.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)因為![]() 的圖象上
的圖象上![]() 、
、![]() 兩點的橫坐標是函數
兩點的橫坐標是函數![]() 的不動點,設
的不動點,設![]() ,
,![]() ,
,
則![]()
直線![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]()
記![]() 的中點
的中點![]() .由(2)知
.由(2)知![]() ,
,
∵![]() 在
在![]() 上,
上,
∴![]() .
.
化簡得
(當且僅當![]() 時,等號成立).
時,等號成立).
即![]() .
.
因為![]() ,所以
,所以![]()
綜上可知![]()
所以![]()


科目:高中數學 來源: 題型:
【題目】如圖,已知平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中,有下列三個命題:
翻折過程中,有下列三個命題:
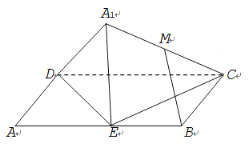
①線段![]() 的長是定值;
的長是定值;
②存在某個位置,使![]() ;
;
③存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題有______. (填寫所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某小區2017年1月至2018年1月當月在售二手房均價(單位:萬元/平方米)的散點圖.(圖中月份代碼1—13分別對應2017年1月—2018年1月)
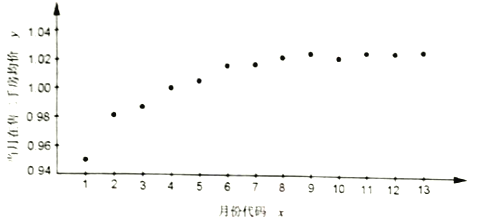
由散點圖選擇![]() 和
和![]() 兩個模型進行擬合,經過數據處理得到兩個回歸方程分別為
兩個模型進行擬合,經過數據處理得到兩個回歸方程分別為![]() 和
和![]() ,并得到以下一些統計量的值:
,并得到以下一些統計量的值:
|
| |
殘差平方和 | 0.000591 | 0.000164 |
總偏差平方和 | 0.006050 | |
(1)請利用相關指數![]() 判斷哪個模型的擬合效果更好;
判斷哪個模型的擬合效果更好;
(2)某位購房者擬于2018年6月份購買這個小區![]() 平方米的二手房(欲
平方米的二手房(欲
購房為其家庭首套房).若購房時該小區所有住房的房產證均已滿2年但未滿5年,請你利用(1)中擬合效果更好的模型估算該購房者應支付的購房金額.(購房金額=房款+稅費;房屋均價精確到0.001萬元/平方米)
附注:根據有關規定,二手房交易需要繳納若干項稅費,稅費是按房屋的計稅價格進行征收.(計稅價格=房款),征收方式見下表:
契稅 (買方繳納) | 首套面積90平方米以內(含90平方米)為1%;首套面積90平方米以上且144平方米以內(含144平方米)為1.5%;面積144平方米以上或非首套為3% |
增值稅 (賣方繳納) | 房產證未滿2年或滿2年且面積在144平方米以上(不含144平方米)為5.6%;其他情況免征 |
個人所得稅 (賣方繳納) | 首套面積144平方米以內(含144平方米)為1%;面積144平方米以上或非首套均為1.5%;房產證滿5年且是家庭唯一住房的免征 |
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 參考公式:相關指數
. 參考公式:相關指數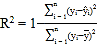 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知定點
中,已知定點![]() ,點
,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 為坐標平面內的動點,且滿足
為坐標平面內的動點,且滿足![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過曲線![]() 第一象限上一點
第一象限上一點![]() (其中
(其中![]() )作切線交直線
)作切線交直線![]() 于點
于點![]() ,連結
,連結![]() 并延長交直線
并延長交直線![]() 于點
于點![]() ,求當
,求當![]() 面積取最小值時切點
面積取最小值時切點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com