
【題目】已知二次函數![]() .
.
(1)畫出函數圖象并寫出頂點坐標和對稱軸;

(2)判斷奇偶性,并指出單調區間.
(3)求函數![]() 在
在![]() 時的值域.
時的值域.
【答案】(1)圖像見解析, 頂點坐標![]() ,對稱軸
,對稱軸![]() (2)
(2)![]() 是非奇非偶函數函數.
是非奇非偶函數函數.![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減(3)見解析
上單調遞減(3)見解析
【解析】
(1)根據函數的解析式作出圖象,根據圖象直接寫出頂點坐標及對稱軸即可;(2)由函數圖象可得函數的奇偶性以及單調區間;(3)分為![]() ,
,![]() 和
和![]() 三種情形,結合單調性得值域.
三種情形,結合單調性得值域.
解:(1)![]()
![]() ,圖象如圖所示:
,圖象如圖所示:
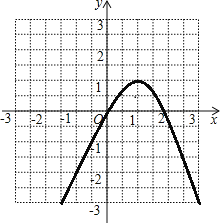
頂點坐標為![]() ,對稱軸為
,對稱軸為![]() .
.
(2)由圖可知:![]() 是非奇非偶函數函數.
是非奇非偶函數函數.
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(3)當![]() 時,
時,![]() 在
在![]() 單調遞增,而
單調遞增,而![]() ,最大值為
,最大值為![]()
∴![]() 的值域為
的值域為![]() ;
;
當![]() 時,
時,![]() 在
在![]() 單調上遞增,在
單調上遞增,在![]() 上單調遞減,
上單調遞減,
而![]() ,最大值為
,最大值為![]() ,
,
∴![]() 的值域為
的值域為![]() ;
;
當![]() 時,
時,![]() 在
在![]() 單調上遞增,在
單調上遞增,在![]() 上單調遞減,
上單調遞減,
最小值為![]() ,最大值為
,最大值為![]() ,
,
∴![]() 的值域為
的值域為![]() ,
,
綜上可得![]() 的值域為:當
的值域為:當![]() 時,值域為
時,值域為![]() ;當
;當![]() ,值域為
,值域為![]() ;當
;當![]() 時,值域為
時,值域為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,短軸長和焦距都等于2,
軸上,短軸長和焦距都等于2,![]() 是橢圓上的一點,且
是橢圓上的一點,且![]() 在第一象限內,過
在第一象限內,過![]() 且斜率等于
且斜率等于![]() 的直線與橢圓
的直線與橢圓![]() 交于另一點
交于另一點![]() ,點
,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() .
.
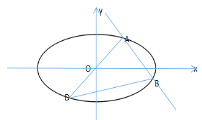
(1)求橢圓![]() 的方程;
的方程;
(2)證明:直線![]() 的斜率為定值;
的斜率為定值;
(3)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2018·江西聯考]交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了80輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
| |
數量 | 20 | 10 | 10 | 20 | 15 | 5 |
以這80輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定,![]() .某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續保時的費用,求X的分布列與數學期望值;(數學期望值保留到個位數字)
.某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續保時的費用,求X的分布列與數學期望值;(數學期望值保留到個位數字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車.假設購進一輛事故車虧損4000元,一輛非事故車盈利8000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只紅鈴蟲的產卵數y和溫度x有關,現收集了6組觀測數據于下表中,通過散點圖可以看出樣本點分布在一條指數型函數y=![]() 的圖象的周圍.
的圖象的周圍.
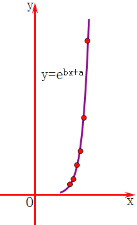
(1)試求出y關于x的上述指數型的回歸曲線方程(結果保留兩位小數);
(2)試用(1)中的回歸曲線方程求相應于點(24,17)的殘差![]() .(結果保留兩位小數)
.(結果保留兩位小數)
溫度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
產卵數y(個) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
幾點說明:
①結果中的![]() 都應按題目要求保留兩位小數.但在求
都應按題目要求保留兩位小數.但在求![]() 時請將
時請將![]() 的值多保留一位即用保留三位小數的結果代入.
的值多保留一位即用保留三位小數的結果代入.
②計算過程中可能會用到下面的公式:回歸直線方程的斜率![]() =
=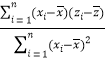 =
=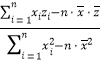 ,截距
,截距![]() .
.
③下面的參考數據可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 為左右焦點,
為左右焦點,![]() 為短軸端點,長軸長為4,焦距為
為短軸端點,長軸長為4,焦距為![]() ,且
,且![]() ,
,![]() 的面積為
的面積為![]() .
.
(Ⅰ)求橢圓![]() 的方程
的方程
(Ⅱ)設動直線![]() 橢圓
橢圓![]() 有且僅有一個公共點
有且僅有一個公共點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() .試探究:在坐標平面內是否存在定點
.試探究:在坐標平面內是否存在定點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在求出點
?若存在求出點![]() 的坐標,若不存在.請說明理由.
的坐標,若不存在.請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的課外閱讀時間情況,某學校隨機抽取了 50人進行統計分析,把這50人每天閱讀的時間(單位:分鐘)繪制成頻數分布表,如下表所示:

若把每天閱讀時間在60分鐘以上(含60分鐘)的同學稱為“閱讀達人”,根據統計結果中男女生閱讀達人的數據,制作出如圖所示的等高條形圖.
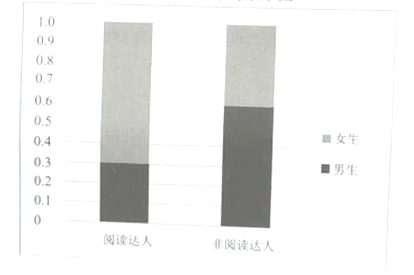
(1)根據抽樣結果估計該校學生的每天平均閱讀時間(同一組數據用該區間的中點值作為代表);
(2)根據已知條件完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“閱讀達人”跟性別有關?
的把握認為“閱讀達人”跟性別有關?
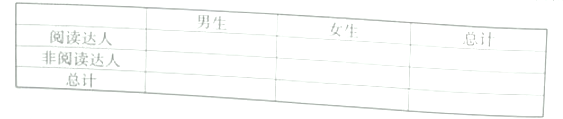
附:參考公式
![]() ,其中
,其中![]() .
.
臨界值表:
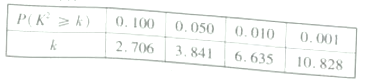
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設E,F分別是正方體ABCD﹣A1B1C1D1的棱DC上兩點,且AB=2,EF=1,給出下列四個命題:
①三棱錐D1﹣B1EF的體積為定值;
②異面直線D1B1與EF所成的角為45°;
③D1B1⊥平面B1EF;
④直線D1B1與平面B1EF所成的角為60°.
其中正確的命題為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com