Question

【題目】在直角坐標(biāo)系中，曲線的參數(shù)方程為（其中為參數(shù)，為的傾斜角，且），曲線的參數(shù)方程為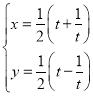（為參數(shù)），以坐標(biāo)原點為極點，軸的正半軸為極軸建立極坐標(biāo)系，曲線的極坐標(biāo)方程為.

（1）求曲線的普通方程及曲線的直角坐標(biāo)方程；

（2）已知點，曲線與交于兩點，與交于點，且，求的普通方程.

Answer 1

【答案】（1）的普通方程為，的直角坐標(biāo)方程為：，（2）或

【解析】

（1）首先給的參數(shù)方程為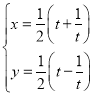平方再相減即可得到的普通方程，根據(jù)直線極坐標(biāo)的形式，即可得到的直角坐標(biāo)方程.

（2）根據(jù)直線參數(shù)方程的幾何意義知：，再將的參數(shù)方程為帶入得到，得到，解方程得到或，即的普通方程為：或.

（1）由題知：，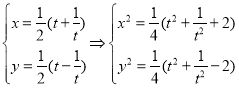

整理得：的普通方程為，

的直角坐標(biāo)方程為：.

（2）的參數(shù)方程為，

對應(yīng)的參數(shù)值為，故.

將的參數(shù)方程為代入得到：

，

整理得：.

，.

因為，所以

即或

因為，所以或

故的普通方程為：或.