
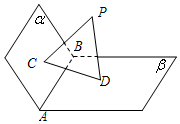
 如圖,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如圖,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.分析 (1)推導出B⊥PC,AB⊥PD從而AB⊥平面PCD,由此能證明AB⊥CD.
(2)過C作CO⊥AB,連結DO,則∠COD是二面角α-AB-β的平面角,推導出PC⊥PD,由此能證明α⊥β.
解答 證明:(1)∵平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足,
∴AB⊥PC,AB⊥PD,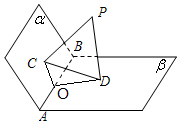
∵PC∩PD=P,
∴AB⊥平面PCD,
∵CD?平面PCD,∴AB⊥CD.
(2)過C作CO⊥AB,連結DO,則DO⊥AB,
∴∠COD是二面角α-AB-β的平面角,
∵PC=PD=1,CD=$\sqrt{2}$,
∴PC2+PD2=CD2,∴PC⊥PD,
∴∠CPD=90°,∴∠COD=90°,
∴α⊥β.
點評 本題考查線線垂直的證明,考查面面垂直的證明,考查空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2e | B. | e | C. | e2 | D. | 2e2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com