【題目】已知圓
，圓
，動圓
與圓
外切并與圓
內切，圓心
的軌跡為曲線
.
（1）求
的方程；
（2）
是與圓
，圓
都相切的一條直線，
與曲線
交于
兩點，當圓
的半徑最長時，求
.
【答案】(1) 
；(2) 
或
.
【解析】
試題分析：對于（1），圓
的圓心為
，半徑
，圓
的圓心為
，半徑
，設圓
的圓心為
，半徑為
，由已知條件不難得到
，進而可得曲線
是以
為左、右焦點，長半軸長為
，短半軸長為
的橢圓，據此即可求出其方程；對于（2），首先根據已知條件圓
的方程，接下來需要分直線
的斜率存在與不存在兩種情況，并結合點到直線的距離公式和弦長公式進行解答即可.
試題解析：由已知得圓的圓心為，半徑；圓的圓心為，半徑，設圓
的圓心為，半徑為.
（1）因為圓
與圓
外切并且與圓
內切，所以
.
由橢圓的定義可知，曲線是以為左、右焦點，長半軸長為，短半軸長為的橢圓（左頂點除外），其方程為.……5分
（2）對于曲線
上任意一點
，由于
，所以
，當且僅當圓
的圓心為
時，
.所以當圓
的半徑最長時，其方程為
.
若
的傾斜角為
，則
與
軸重合，可得
.
若
的傾斜角不為，由
知
不平行于
軸，設
與
軸的交點為
，
則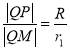
，可求得
，所以可設
.由
與圓
相切得
，解得
.
當
時，將
帶入
，并整理得
，
解得
.所以
.
當
時，由圖形的對稱性可知
.綜上，或.……12分
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn，
，Sn＝n2an－n(n－1)，n＝1，2，…
(1)證明：數列{
Sn}是等差數列，并求Sn；
(2)設
，求證 ：b1＋b2＋…＋bn＜1．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出x與銷售額y(單位：百萬元)之間有如下的對應數據：
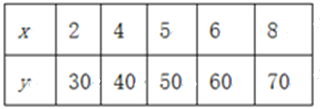
（1）請畫出上表數據的散點圖；
（2）請根據上表提供的數據，用最小二乘法求出y關于x的線性回歸方程
=
x+
；
（參考公式：用最小二乘法求線性回歸方程系數公式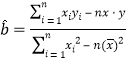 
，
．）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）是定義在R上的偶函數，且對任意的x∈R，都有f（x+2）=f（x）．當0≤x≤1時，f（x）=x2．若直線y=x+a與函數y=f（x）的圖象有兩個不同的公共點，則實數a的值為（ ）
A. n（n∈Z） B. 2n（n∈Z）
C. 2n或
（n∈Z） D. n或
（n∈Z）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝2x＋1，x∈N*.若x0，n∈N*，使f(x0)＋f(x0＋1)＋…＋f(x0＋n)＝63成立，則稱(x0，n)為函數f(x)的一個“生成點”．則函數f(x)的“生成點”共有( )
A．1個 B．2個 C．3個 D．4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知三棱錐P—ABC中，PC
底面ABC，AB=BC，D、F分別為AC、PC的中點，DEAP于E。（1）求證：AP平面BDE；（2）求證：平面BDE平面BDF；（3）若AE：EP=1：2，求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
