
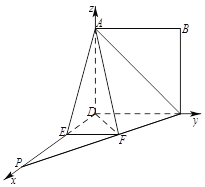
【題目】如圖4,四邊形![]() 為正方形,
為正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 于點
于點![]() ,
,![]() ,交
,交![]() 于點
于點![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:(1)由![]() 平面
平面![]() ,得到
,得到![]() ,再由四邊形
,再由四邊形![]() 為正方形得到
為正方形得到![]() ,從而證明
,從而證明![]() 平面
平面![]() ,從而得到
,從而得到![]() ,再結合
,再結合![]() ,即
,即![]() 以及直線與平面垂直的判定定理證明
以及直線與平面垂直的判定定理證明![]() 平面
平面![]() ;(2)先證明
;(2)先證明![]() 、
、![]() 、
、![]() 三條直線兩兩垂直,然后以點
三條直線兩兩垂直,然后以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系,利用空間向量法求出二面角
軸建立空間直角坐標系,利用空間向量法求出二面角![]() 的余弦值.
的余弦值.
試題解析:(1)![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ;
;
(2)設![]() ,則
,則![]() 中,
中,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,由(1)知
,由(1)知![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,同理
,同理![]() ,
,
如圖所示,以![]() 為原點,建立空間直角坐標系,則
為原點,建立空間直角坐標系,則![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設![]() 是平面
是平面![]() 的法向量,則
的法向量,則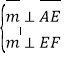 ,又
,又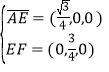 ,
,
所以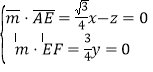 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
由(1)知平面![]() 的一個法向量
的一個法向量![]() ,
,
設二面角![]() 的平面角為
的平面角為![]() ,可知
,可知![]() 為銳角,
為銳角,
![]()
![]() ,即所求.
,即所求.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖所示,在空間直角坐標系![]() 的坐標平面
的坐標平面![]() 內,若函數
內,若函數 的圖象與
的圖象與![]() 軸圍成一個封閉區域
軸圍成一個封閉區域![]() ,將區域
,將區域![]() 沿
沿![]() 軸的正方向上移4個單位,得到幾何體如圖一.現有一個與之等高的圓柱如圖二,其底面積與區域
軸的正方向上移4個單位,得到幾何體如圖一.現有一個與之等高的圓柱如圖二,其底面積與區域![]() 面積相等,則此圓柱的體積為__________.
面積相等,則此圓柱的體積為__________.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知向量 ![]() =(2sinA,cos(A﹣B)),
=(2sinA,cos(A﹣B)), ![]() =(sinB,﹣1),且
=(sinB,﹣1),且 ![]()
![]() =
= ![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ![]() ,求b﹣a的取值范圍.
,求b﹣a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我校對高二600名學生進行了一次知識測試,并從中抽取了部分學生的成績(滿分100分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.
(1)填寫頻率分布表中的空格,補全頻率分布直方圖,并標出每個小矩形對應的縱軸數據;
分組 | 頻數 | 頻率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合計 | 1.00 |
如果用分層抽樣的方法從樣本分數在[60,70)和[80,90)的人中共抽取6人,再從6人中選2人,求2人分數都在[80,90)的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一裝有水的直三棱柱![]() 容器(厚度忽略不計),上下底面均為邊長為5的正三角形,側棱為10,側面
容器(厚度忽略不計),上下底面均為邊長為5的正三角形,側棱為10,側面![]() 水平放置,如圖所示,點
水平放置,如圖所示,點![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別在棱
分別在棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 上,水面恰好過點
上,水面恰好過點![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)證明: ![]() ;
;
(2)若底面![]() 水平放置時,求水面的高.
水平放置時,求水面的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的不等式|x+1|+|x﹣1|<4的解集為M.
(1)設Z是整數集,求Z∩M;
(2)當a,b∈M時,證明:2|a+b|<|4+ab|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=3sinx+2cosx+1.若實數a,b,c使得af(x)+bf(x﹣c)=1對任意實數x恒成立,則 ![]() 的值為( )
的值為( )
A.﹣1
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取一個年份,對西安市該年4月份的天氣情況進行統計,結果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天氣 | 晴 | 雨 | 陰 | 陰 | 陰 | 雨 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天氣 | 晴 | 陰 | 雨 | 陰 | 陰 | 晴 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估計西安市在該天不下雨的概率;
(2)西安市某學校擬從4月份的一個晴天開始舉行連續2天的運動會,估計運動會期間不下雨的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com