
| A. | $\frac{1}{{e}^{2}}$ | B. | 2(ln2-1) | C. | $\frac{4}{{e}^{2}}$ | D. | ln2-1 |
分析 求出f(f(x))的解析式,根據f(f(x))的函數圖象判斷x1,x2的范圍和兩根的關系,構造函數h(x1)=e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$,求出h(x1)的最大值即可.
解答 解:令g(x)=f(f(x))=$\left\{\begin{array}{l}{{e}^{{e}^{x}},x≥0}\\{{e}^{{x}^{2}},x<0}\end{array}\right.$,
∵y=f(x)在(-∞,0)上單調遞減,在[0,+∞)上單調遞增,
∴g(x)=f(f(x))在(-∞,0)上單調遞減,在[0,+∞)上單調遞增.
做出g(x)=f(f(x))的函數圖象如圖所示: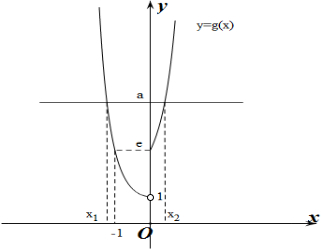
∵方程f(f(x))=a(a>0)恰有兩個不相等的實根x1,x2,
不妨設x1<x2,則x1≤-1,x2≥0,且f(x1)=f(x2),即x12=e${\;}^{{x}_{2}}$.
∴e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$=e${\;}^{{x}_{1}}$•x12,
令h(x1)=e${\;}^{{x}_{1}}$•x12,則h′(x1)=e${\;}^{{x}_{1}}$(x12+2x1)=e${\;}^{{x}_{1}}$•x1•(x1+2),
∴當x1<-2時,h′(x1)>0,當-2<x1<-1時,h′(x1)<0,
∴h(x1)在(-∞,-2)上單調遞增,在(-2,-1)上單調遞減,
∴當x1=-2時,h(x1)取得最大值h(-2)=$\frac{4}{{e}^{2}}$.
故選C.
點評 本題考查了根的個數與函數圖象的關系,函數單調性判斷與函數最值的計算,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (30,42] | B. | (20,30) | C. | (20,30] | D. | (20,42) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
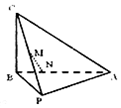 如圖,在三棱錐C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,點M是PC的中點,點N在線段AB上,且MN⊥AB.
如圖,在三棱錐C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,點M是PC的中點,點N在線段AB上,且MN⊥AB.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
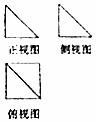 如圖是一個幾何體的三視圖,其中正視圖和側視圖是腰長為1的兩個全等的等腰直角三角形,則該多面體的各條棱中最長棱的長度為( )
如圖是一個幾何體的三視圖,其中正視圖和側視圖是腰長為1的兩個全等的等腰直角三角形,則該多面體的各條棱中最長棱的長度為( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com