
(本小題滿分14分)如圖,有三個生活小區(qū)(均可看成點)分別位于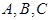 三點處,
三點處,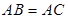 ,
,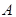 到線段
到線段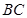 的距離
的距離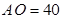 ,
,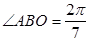 (參考數(shù)據(jù):
(參考數(shù)據(jù): 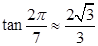 ). 今計劃建一個生活垃圾中轉站
). 今計劃建一個生活垃圾中轉站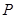 ,為方便運輸,
,為方便運輸,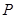 準備建在線段
準備建在線段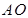 (不含端點)上.
(不含端點)上.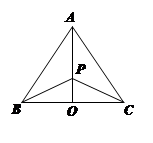
(1)設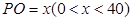 ,試將
,試將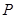 到三個小區(qū)距離的最遠者
到三個小區(qū)距離的最遠者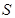 表示為
表示為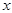 的函數(shù),并求
的函數(shù),并求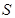 的最小值;
的最小值;
(2)設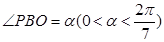 ,試將
,試將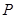 到三個小區(qū)的距離之和
到三個小區(qū)的距離之和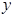 表示為
表示為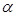 的函數(shù),并確定當
的函數(shù),并確定當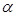 取何值時,可使
取何值時,可使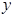 最小?
最小?
(1)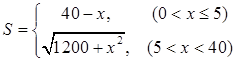 當
當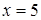 時,
時,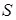 取得小值為35
取得小值為35
(2)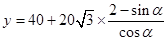 ,當
,當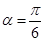 時,
時,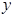 最小
最小
解析試題分析:(1)在 中,因為
中,因為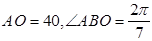 ,所以
,所以 ,
,
所以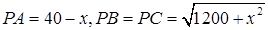 ………………………………2分
………………………………2分
①若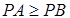 ,即
,即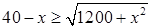 ,即
,即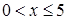 時,
時, 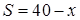 ;
;
②若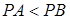 ,即
,即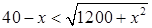 ,即
,即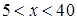 時,
時, 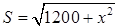 .
.
從而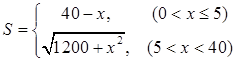 …………………………………………4分
…………………………………………4分
當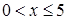 時,
時,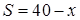 在
在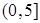 上是減函數(shù),∴
上是減函數(shù),∴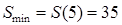 ;
;
當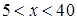 時,
時,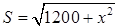 在
在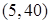 上是增函數(shù),∴
上是增函數(shù),∴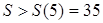 ,
,
綜上所述,當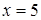 時,
時,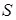 取得小值為35………………………………………7分
取得小值為35………………………………………7分
(2)在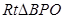 中,
中, 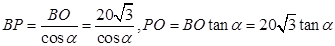 ……………………9分
……………………9分
又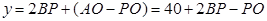 ,
,
所以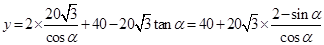 ………………………11分
………………………11分
因為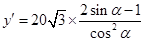 ,令
,令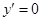 ,即
,即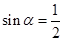 ,從而
,從而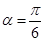 ,
,
當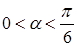 時,
時,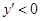 ;當
;當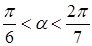 時,
時, 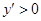 .
.
∴當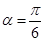 時,可使
時,可使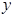 最小……………………………………14分
最小……………………………………14分
考點:分段函數(shù),利用導數(shù)求函數(shù)最值
點評:本題難度較大,第二問中求y最值不易想到導數(shù)工具


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案科目:高中數(shù)學 來源: 題型:解答題
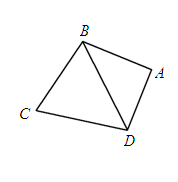
(本小題滿分12分)如圖4平面四邊形ABCD中,AB=AD=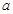 ,BC=CD=BD,設
,BC=CD=BD,設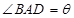 .
.
(1)將四邊形ABCD的面積S表示為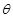 的函數(shù);
的函數(shù);
(2)求四邊形ABCD面積S的最大值及此時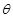 值.
值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分10分) 如圖,在平行四邊形 中,
中, ,將
,將 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求二面角E-AB-D的大小;
(2)求四面體 的表面積和體積.
的表面積和體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,已知正方形ABCD的邊長為1,F(xiàn)D⊥平面ABCD,EB⊥平面ABCD,F(xiàn)D=BE=1,M為BC邊上的動點.
(1)設N為EF上一點,當 時,有DN ∥平面AEM,求
時,有DN ∥平面AEM,求  的值;
的值;
(2)試探究點M的位置,使平面AME⊥平面AEF。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分12分)
如圖1,在三棱錐P-A.BC中,PA.⊥平面A.BC,A.C⊥BC,D為側棱PC上一點,它的正(主)視圖和側(左)視圖如圖2所示.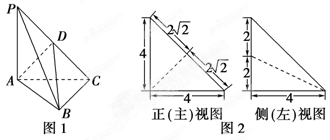
(1) 證明:A.D⊥平面PBC;
(2) 求三棱錐D-A.BC的體積;
(3) 在∠A.CB的平分線上確定一點Q,使得PQ∥平面A.BD,并求此時PQ的長.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com