【題目】某校為了了解學生對電子競技的興趣，從該校高二年級的學生中隨機抽取了
人進行檢查，已知這人中有
名男生對電子競技有興趣，而對電子競技沒興趣的學生人數與電子競技競技有興趣的女生人數一樣多，且女生中有
的人對電子競技有興趣.
在被抽取的女生中與
名高二
班的學生，其中有
名女生對電子產品競技有興趣，先從這名學生中隨機抽取人，求其中至少有
人對電子競技有興趣的概率；
完成下面的
列聯表，并判斷是否有
的把握認為“電子競技的興趣與性別有關”.
有興趣 | 沒興趣 | 合計 | |
男生 | |||
女生 | |||
合計 |
參考數據：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：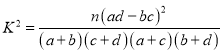
【答案】
；
列聯表見解析，沒有.
【解析】
（1）計算出從
名學生中隨機抽取
人的可能，再計算出抽到的人中至少有
人對電子競技有興趣的可能，利用古典概型公式即得答案；
（2）先填寫列聯表，然后計算
，與
比較大小即可得到答案.
從名學生中隨機抽取人，共有
種不同的抽取方案；抽到的人中至少有人對電子競技有興趣的方案數有：
種
抽取人中至少有人對電子競技有興趣的概率為
.
設對電子競技沒興趣的學生人數為
，
對電子競技沒興趣的學生人數與對電子競技有興趣的女生人數一樣多
由題
，解得
.
又女生中有
的人對電子競技有興趣，
女生人數為
男生人數為
，其中有
人對電子競技沒興趣
得到下面列聯表
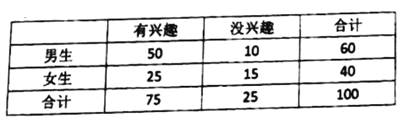
沒用
的把握認為“對電子競技的興趣與性別有關”.
新思維寒假作業系列答案科目：高中數學 來源： 題型：
【題目】給出以下命題：
①雙曲線
的漸近線方程為y＝±
x；
②命題p：“x∈R，sinx＋
≥2”是真命題；
③已知線性回歸方程為
＝3＋2x，當變量x增加2個單位，其預報值平均增加4個單位；
④設隨機變量ξ服從正態分布N(0,1)，若P(ξ>1)＝0.2，則P(－1<ξ<0)＝0.6；
⑤設
，則
則正確命題的序號為________(寫出所有正確命題的序號)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】雙曲線
的左、右焦點分別為
、
，直線
過且與雙曲線交于
、
兩點．
（1）若的傾斜角為
，
，
是等腰直角三角形，求雙曲線的標準方程；
（2），
，若的斜率存在，且
，求的斜率；
（3）證明：點
到已知雙曲線的兩條漸近線的距離的乘積為定值
是該點在已知雙曲線上的必要非充分條件．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數角度看，
可以看成是以
為自變量的函數
，其定義域是
.
（1）證明：
（2）試利用1的結論來證明：當
為偶數時，
的展開式最中間一項的二項式系數最大；當為奇數時的展開式最中間兩項的二項式系數相等且最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
