
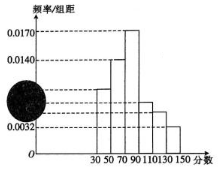
 2017年省內事業單位面向社會公開招聘工作人員,為保證公平競爭,報名者需要參加筆試和面試兩部分,且要求筆試成績必須大于或等于90分的才有資格參加面試,90分以下(不含90分)則被淘汰.現有2000名競聘者參加筆試,參加筆試的成績按區間[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其頻率分布直方圖如下圖所示(頻率分布直方圖有污損),但是知道參加面試的人數為500,且筆試成績在的人數為1440.
2017年省內事業單位面向社會公開招聘工作人員,為保證公平競爭,報名者需要參加筆試和面試兩部分,且要求筆試成績必須大于或等于90分的才有資格參加面試,90分以下(不含90分)則被淘汰.現有2000名競聘者參加筆試,參加筆試的成績按區間[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其頻率分布直方圖如下圖所示(頻率分布直方圖有污損),但是知道參加面試的人數為500,且筆試成績在的人數為1440.分析 (1)求出競聘者成績在區間[30,50),[90,110),[110,130)的人數,由此能求出競聘者參加筆試的平均成績.
(2)設面試者甲每道題答對的概率為p,則${C}_{3}^{1}p(1-p)^{2}$=$\frac{9}{64}$,解得p=$\frac{3}{4}$,面試者甲答題個數X的可能取值為3,4,5,分別求出相應的概率,由此能求出X的人布列和E(X).
解答 解:(1)設競聘者成績在區間[30,50),[90,110),[110,130)的人數分別為x,y,z,
則(0.0170+0.0140)×20×2000+x=2000-500,解得x=260,
(0.0170+0.0140)×20×2000+y=1440,解得y=200,
0.0032×20×2000+200+z=500,解得z=172,
競聘者參加筆試的平均成績為:
$\frac{1}{2000}$×(260×40+200×100+172×120)+(0.014×60+0.017×80+0.0032×140)×20=78.48(分).
(2)設面試者甲每道題答對的概率為p,則${C}_{3}^{1}p(1-p)^{2}$=$\frac{9}{64}$,解得p=$\frac{3}{4}$,
面試者甲答題個數X的可能取值為3,4,5,
則P(X=3)=($\frac{3}{4}$)3+($\frac{1}{4}$)3=$\frac{7}{16}$,
P(X=4)=${C}_{3}^{2}(\frac{1}{4})(\frac{3}{4})^{2}+{C}_{3}^{1}(\frac{3}{4})(\frac{1}{4})^{2}(\frac{1}{4})=\frac{45}{128}$,
P(X=5)=1-P(X=3)-P(X=4)=1-$\frac{7}{16}$-$\frac{45}{128}$=$\frac{27}{128}$,
∴X的人布列為:
| X | 3 | 4 | 5 |
| P | $\frac{7}{16}$ | $\frac{45}{128}$ | $\frac{27}{128}$ |
點評 本題考查頻率分布直方圖的應用,考查離散型隨機變量的分布列、數學期望的求法,考查運算求解能力、數據處理能力,考查數形結合思想,是中檔題.


科目:高中數學 來源: 題型:解答題
 已知正三棱柱ABC-A1B1C1所有棱長均為2,D、E分別是BC、BB1中點.
已知正三棱柱ABC-A1B1C1所有棱長均為2,D、E分別是BC、BB1中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com