
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 可畫出圖形,根據條件及${\overrightarrow{BC}}^{2}=(\overrightarrow{AC}-\overrightarrow{AB})^{2}$即可求出${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=20$,然后根據$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$即可求出${\overrightarrow{AD}}^{2}$的值,從而得出$|\overrightarrow{AD}|$的值.
解答 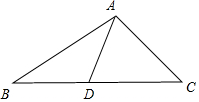 解:如圖,
解:如圖,
$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$;
∴${\overrightarrow{BC}}^{2}=(\overrightarrow{AC}-\overrightarrow{AB})^{2}$
=${\overrightarrow{AC}}^{2}-2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AB}}^{2}$
=${\overrightarrow{AC}}^{2}+16+{\overrightarrow{AB}}^{2}$
=36;
∴${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=20$;
∴${\overrightarrow{AD}}^{2}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})^{2}$
=$\frac{1}{4}({\overrightarrow{AB}}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2})$
=$\frac{1}{4}(20-16)$
=1;
∴$|\overrightarrow{AD}|=1$.
故選D.
點評 考查向量減法的幾何意義,向量加法的平行四邊形法則,以及向量數量積的運算,要求$|\overrightarrow{AD}|$,而求${\overrightarrow{AD}}^{2}$的方法.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
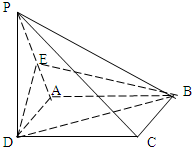 如圖:已知四棱錐P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中點,
如圖:已知四棱錐P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中點,查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,∠ADC=45°,AD=
如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,∠ADC=45°,AD=查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
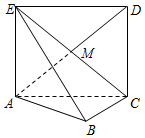 如圖,正方形ACDE所在的平面與平面ABC垂直,M是CE和AD的交點,AC⊥BC,且AC=BC=2
如圖,正方形ACDE所在的平面與平面ABC垂直,M是CE和AD的交點,AC⊥BC,且AC=BC=2查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com