設復數Z=lg（m2-2m-14）+（m2+4m+3）i，試求實數m為何值時
（1）Z是純虛數 （2）Z對應點位于復平面的第二象限．
解：（1）∵復數Z=lg（m
2-2m-14）+（m
2+4m+3）i，當Z是純虛數時，
應有 lg（m
2-2m-14）=0，且m
2+4m+3≠0． 即m
2-2m-14=1，且m≠-1，m≠-3．
解得 m=5．
（2）當Z對應點位于復平面的第二象限時，lg（m
2-2m-14）＜0，且m
2+4m+3＞0，
即 0＜m
2-2m-14＜1，且m
2+4m+3＞0，解得
．
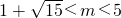
分析：（1）由純虛數的定義可得lg（m
2-2m-14）=0，且m
2+4m+3≠0，由此求得實數m的值．
（2）當Z對應點位于復平面的第二象限時，lg（m
2-2m-14）＜0，且m
2+4m+3＞0，求得實數m的值．
點評：本題主要考查復數的基本概念，一元二次不等式的解法，屬于基礎題．
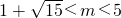閱讀快車系列答案