
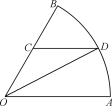
【題目】如圖1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 上一點,且
上一點,且![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,現將
,現將![]() 沿
沿![]() 折到
折到![]() ,使
,使![]() ,如圖2.
,如圖2.
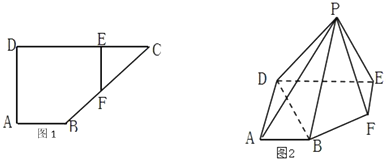
(1)求證:![]() 平面
平面![]()
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
【答案】(1)證明見解析;(2)不存在,理由見解析
【解析】
(1)解法一:由![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ,即有
,即有![]() 平面
平面![]() ,故
,故![]() ,結合
,結合![]() 即可推出
即可推出![]() 平面
平面![]() ;解法二:建立空間直角坐標系,利用向量推出結論;
;解法二:建立空間直角坐標系,利用向量推出結論;
(2)由(1)知![]() 平面
平面![]() ,故以
,故以![]() 所在的直線為
所在的直線為![]() 軸,以
軸,以![]() 所在的直線為
所在的直線為![]() 軸,在平面
軸,在平面![]() 內過
內過![]() 作
作![]() 的垂線,以垂線所在直線為
的垂線,以垂線所在直線為![]() 軸,建立空間直角坐標系,設
軸,建立空間直角坐標系,設![]() 是線段
是線段![]() 上一點,則存在
上一點,則存在![]() ,使
,使![]() ,再利用向量,結合線面角公式列式求解即可.
,再利用向量,結合線面角公式列式求解即可.
(1)解法一:
∵![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又直角梯形![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
則![]() 平面
平面![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又因為直線![]() ,
,![]() 在平面
在平面![]() 內,且相交于
內,且相交于![]() ,∴
,∴![]() 平面
平面![]() .
.
解法二:
以為![]() ,
,![]() ,且
,且![]() ,
,
則![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
以![]() 所在的直線為
所在的直線為![]() 軸,以
軸,以![]() 所在的直線為
所在的直線為![]() 軸,在平面
軸,在平面![]() 內過
內過![]() 作
作![]()
的垂線,以垂線所在直線為![]() 軸,建立空間直角坐標系,如圖所示:
軸,建立空間直角坐標系,如圖所示:
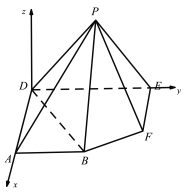
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() 是平面
是平面![]() 內的相交直線,
內的相交直線,
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
以![]() 所在的直線為
所在的直線為![]() 軸,以
軸,以![]() 所在的直線為
所在的直線為![]() 軸,在平面
軸,在平面![]() 內過
內過![]() 作
作![]() 的垂線,以垂線所在直線為
的垂線,以垂線所在直線為![]() 軸,建立空間直角坐標系,如圖所示:
軸,建立空間直角坐標系,如圖所示:
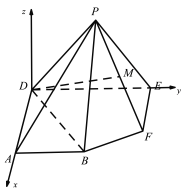
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一個法向量為
的一個法向量為![]() ,
,
設![]() 是線段
是線段![]() 上一點,則存在
上一點,則存在![]() ,使
,使![]() ,
,
∴![]()
![]() ,
,
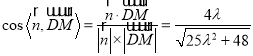 ,
,
如果直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
那么![]() ,即
,即![]() ,
,
解得![]() ,此方程在
,此方程在![]() 內無解,
內無解,
所以在線段![]() 上不存在一點
上不存在一點![]() ,使
,使![]() 與平在
與平在![]() 所成的角為
所成的角為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖是一個半徑為2千米,圓心角為![]() 的扇形游覽區的平面示意圖
的扇形游覽區的平面示意圖![]() 是半徑
是半徑![]() 上一點,
上一點,![]() 是圓弧
是圓弧![]() 上一點,且
上一點,且![]() .現在線段
.現在線段![]() ,線段
,線段![]() 及圓弧
及圓弧![]() 三段所示位置設立廣告位,經測算廣告位出租收入是:線段
三段所示位置設立廣告位,經測算廣告位出租收入是:線段![]() 處每千米為
處每千米為![]() 元,線段
元,線段![]() 及圓弧
及圓弧![]() 處每千米均為
處每千米均為![]() 元.設
元.設![]() 弧度,廣告位出租的總收入為
弧度,廣告位出租的總收入為![]() 元.
元.
(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)試問:![]() 為何值時,廣告位出租的總收入最大?并求出其最大值.
為何值時,廣告位出租的總收入最大?并求出其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
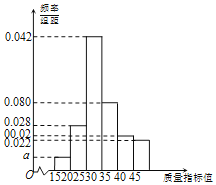
【題目】為保障食品安全,某地食品藥監管部門對轄區內甲、乙兩家食品企業進行檢查,分別從這兩家企業生產的某種同類產品中隨機抽取了100件作為樣本,并以樣本的一項關鍵質量指標值為檢測依據.已知該質量指標值對應的產品等級如下:
質量指標值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等級 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
根據質量指標值的分組,統計得到了甲企業的樣本頻率分布直方圖和乙企業的樣本頻數分布表(如下面表,其中a>0).
質量指標值 | 頻數 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合計 | 100 |
(Ⅰ)現從甲企業生產的產品中任取一件,試估計該件產品為次品的概率;
(Ⅱ)為守法經營、提高利潤,乙企業開展次品生產原因調查活動.已知乙企業從樣本里的次品中隨機抽取了兩件進行分析,求這兩件次品中恰有一件指標值屬于[40,45]的產品的概率;
(Ⅲ)根據圖表數據,請自定標準,對甲、乙兩企業食品質量的優劣情況進行比較.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要排出高三某班一天中,語文、數學、英語各![]() 節,自習課
節,自習課![]() 節的功課表,其中上午
節的功課表,其中上午![]() 節,下午
節,下午![]() 節,若要求
節,若要求![]() 節語文課必須相鄰且
節語文課必須相鄰且![]() 節數學課也必須相鄰(注意:上午第五節和下午第一節不算相鄰),則不同的排法種數是( )
節數學課也必須相鄰(注意:上午第五節和下午第一節不算相鄰),則不同的排法種數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() ,
,![]() ,
,![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)若對![]() ,都有
,都有![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)當![]() 時,將數列
時,將數列![]() 中的部分項按原來的順序構成數列
中的部分項按原來的順序構成數列![]() 且
且![]() 證明:存在無數個滿足條件的無窮等比數列
證明:存在無數個滿足條件的無窮等比數列![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是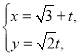 (
(![]() 為參數),曲線
為參數),曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,將曲線
,將曲線![]() 上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線
上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線![]() .
.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 和曲線
和曲線![]() 相交于
相交于![]() 兩點,求三角形
兩點,求三角形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() ,若滿足
,若滿足![]() (
(![]() 且
且![]() ),對于任意的
),對于任意的![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為“指數型數列”.
為“指數型數列”.
(1)已知數列![]() 的通項公式為
的通項公式為![]() ,試判斷數列
,試判斷數列![]() 是不是“指數型數列”;
是不是“指數型數列”;
(2)已知數列![]() 滿足
滿足![]() ,
,![]() ,證明數列
,證明數列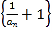 為等比數列,并判斷數列
為等比數列,并判斷數列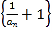 是否為“指數型數列”,若是給出證明,若不是說明理由;
是否為“指數型數列”,若是給出證明,若不是說明理由;
(3)若數列![]() 是“指數型數列”,且
是“指數型數列”,且![]() ,證明數列
,證明數列![]() 中任意三項都不能構成等差數列.
中任意三項都不能構成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的長軸是短軸的兩倍,點
的長軸是短軸的兩倍,點![]() 在橢圓上.不過原點的直線
在橢圓上.不過原點的直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,設直線
兩點,設直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好構成等比數列,
恰好構成等比數列,
(1)求橢圓![]() 的方程;
的方程;
(2)試判斷![]() 是否為定值?若是,求出這個值;若不是,請說明理由?
是否為定值?若是,求出這個值;若不是,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了豐富學生的課外文體活動,分別開設了閱讀、書法、繪畫等文化活動;跑步、游泳、健身操等體育活動.該中學共有高一學生300名,要求每位學生必須選擇參加其中一項活動,現對高一學生的性別、學習積極性及選擇參加的文體活動情況進行統計,得到數據如下:

(1)在選擇參加體育活動的學生中按性別分層抽取6名,再從這6名學生中抽取2人了解家庭情況,求2人中至少有1名女生的概率;
(2)是否有99.9%的把握認為學生的學習積極性與選擇參加文化活動有關?請說明你的理由.
附:參考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com