
【題目】為保障食品安全,某地食品藥監管部門對轄區內甲、乙兩家食品企業進行檢查,分別從這兩家企業生產的某種同類產品中隨機抽取了100件作為樣本,并以樣本的一項關鍵質量指標值為檢測依據.已知該質量指標值對應的產品等級如下:
質量指標值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等級 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
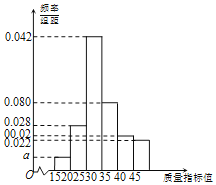
根據質量指標值的分組,統計得到了甲企業的樣本頻率分布直方圖和乙企業的樣本頻數分布表(如下面表,其中a>0).
質量指標值 | 頻數 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合計 | 100 |
(Ⅰ)現從甲企業生產的產品中任取一件,試估計該件產品為次品的概率;
(Ⅱ)為守法經營、提高利潤,乙企業開展次品生產原因調查活動.已知乙企業從樣本里的次品中隨機抽取了兩件進行分析,求這兩件次品中恰有一件指標值屬于[40,45]的產品的概率;
(Ⅲ)根據圖表數據,請自定標準,對甲、乙兩企業食品質量的優劣情況進行比較.
【答案】(Ⅰ)0.14(Ⅱ)![]() (Ⅲ)乙
(Ⅲ)乙
【解析】
(Ⅰ)由頻率分布直方圖求出a=0.008,從而甲企業的樣本中次品的頻率為0.14,由此能求出從甲企業生產的產品中任取一件,該產品是次品的概率.
(Ⅱ)記“從乙企業樣本里的次品中任取兩件產品,恰有一件產品是指標值屬于[40,45]的產品”為事件M,記質量指標值在[15,20]內的2件產品的樣本分別為A1,A2,質量指標值在[40,45]內的確件產品樣本分別為B1,B2,從乙企業樣本中的次品中任取兩件產品,所有可能結果有6種,由此能求出這兩件次品中恰有一件指標值屬于[40,45]的產品的概率.
(Ⅲ)以產品的合格率(非次品的占有率)為標準,對甲、乙兩家企業的產品質量進行比較,得到乙企業產品的食品生產質量更高.
解:(Ⅰ)由頻率分布直方圖得:
(a+0.020+0.022+0.028+0.042+0.080)×5=1,
解得a=0.008,
∴甲企業的樣本中次品的頻率為(a+0.020)×5=0.14,
故從甲企業生產的產品中任取一件,該產品是次品的概率為0.14.
(Ⅱ)記“從乙企業樣本里的次品中任取兩件產品,恰有一件產品是指標值屬于[40,45]的產品”為事件M,
記質量指標值在[15,20]內的2件產品的樣本分別為A1,A2,質量指標值在[40,45]內的確件產品樣本分別為B1,B2,
從乙企業樣本中的次品中任取兩件產品,所有可能結果有6種,分別為:
(A1,A2),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(B1,B2),
而事件M包含的結果有4種,分別為:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),
∴這兩件次品中恰有一件指標值屬于[40,45]的產品的概率P=![]() .
.
(Ⅲ)以產品的合格率(非次品的占有率)為標準,對甲、乙兩家企業的產品質量進行比較,
由圖表可知甲企業產品的合格率約為0.86,乙企業產品的合格率約為0.96,
即乙企業產品的合格率高于甲企業產品的合格率,
∴認為乙企業產品的食品生產質量更高.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】設點![]() 為拋物線
為拋物線![]() 外一點,過點
外一點,過點![]() 作拋物線
作拋物線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,切點分別為
,切點分別為![]() ,
,![]() .
.

(Ⅰ)若點![]() 為
為![]() ,求直線
,求直線![]() 的方程;
的方程;
(Ⅱ)若點![]() 為圓
為圓![]() 上的點,記兩切線
上的點,記兩切線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有9張各寫有一個數字的卡片,其中4張卡片上的數字是1,3張卡片上的數字是2,2張卡片上的數字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數字完全相同的概率;
(2)![]() 表示所取3張卡片上的數字的中位數,求
表示所取3張卡片上的數字的中位數,求![]() 的分布列與數學期望.
的分布列與數學期望.
(注:若三個數![]() 滿足
滿足![]() ,則稱
,則稱![]() 為這三個數的中位數).
為這三個數的中位數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系 xOy 中,已知橢圓 C:![]() 的離心率為
的離心率為![]() ,且過點 (
,且過點 (![]() ,
,![]() ),點 P 在第四象限, A 為左頂點, B 為上頂點, PA 交 y 軸于點 C,PB 交 x 軸于點 D.
),點 P 在第四象限, A 為左頂點, B 為上頂點, PA 交 y 軸于點 C,PB 交 x 軸于點 D.

(1) 求橢圓 C 的標準方程;
(2) 求 △PCD 面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在各項均為正數的等比數列{an}中,![]() ,且a4+a5=6a3.
,且a4+a5=6a3.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設數列{log2an}的前n項和為Sn,求Sn的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學有學生500人,學校為了解學生的課外閱讀時間,從中隨機抽取了50名學生,獲得了他們某一個月課外閱讀時間的數據(單位:小時),將數據分為5組:[10,12),[12,14),[14,16),[16,18),[18,20],整理得到如圖所示的頻率分布直方圖.
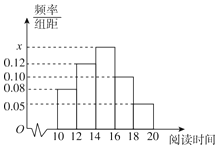
(1)求頻率分布直方圖中的x的值;
(2)試估計該校所有學生中,課外閱讀時間不小于16小時的學生人數;
(3)已知課外閱讀時間在[10,12)的樣本學生中有3名女生,現從閱讀時間在[10,12)的樣本學生中隨機抽取3人,記X為抽到女生的人數,求X的分布列與數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (a,b
(a,b![]() R).
R).
(1)當a=b=1時,求![]() 的單調增區間;
的單調增區間;
(2)當a≠0時,若函數![]() 恰有兩個不同的零點,求
恰有兩個不同的零點,求![]() 的值;
的值;
(3)當a=0時,若![]() 的解集為(m,n),且(m,n)中有且僅有一個整數,求實數b的取值范圍.
的解集為(m,n),且(m,n)中有且僅有一個整數,求實數b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com