【題目】數列
滿足
若
，則數列的前
項的和是__________．
【答案】450
【解析】分析：根據遞推關系求出數列
的前幾項，不難發現項的變化具有周期性，從而得到數列的前
項的和.
詳解：∵數列{an}滿足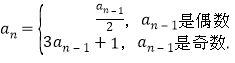
，
∵a1=34，∴a2=
=17，a3=3a2+1=3×17+1=52，a4=
=26，a5=
=13，a6=3a5+1=40，a7=
=20，a8=
=10，a9=
=5，a10=3a9+1=16，
a11=
=8，a12=
=4，a13=
=2，a14=
=1，同理可得：a15=4，a16=2，a17=1，……．
可得此數列從第12項開始為周期數列，周期為3．
則數列{an}的前100項的和=（a1+a2+……+a11）+a12+a13+29（a14+a15+a16）
=（34+17+52+26+13+40+20+10+5+16+8）+4+2+29×（1+4+2）
=450．
故答案為：450．
名師伴你成長課時同步學練測系列答案科目：高中數學 來源： 題型：
【題目】定義：由橢圓的兩個焦點和短軸的一個頂點組成的三角形稱為該橢圓的“特征三角形”；如果兩個橢圓的“特征三角形”是相似的，則稱這兩個橢圓是“相似橢圓”，并將三角形的相似比稱為橢圓的相似比，已知橢圓
.
（1）若橢圓
，判斷
與
相似？如果相似，求出與的相似比；如果不相似，請說明理由；
（2）寫出與橢圓相似且焦點在
軸上，短半軸長為
的橢圓
的標準方程；若在橢圓上存在兩點
、
關于直線
對稱，求實數的取值范圍；
（3）如圖：直線
與兩個“相似橢圓”
和
分別交于點
和點
，試在橢圓和橢圓
上分別作出點
和點
（非橢圓頂點），使
和
組成以
為相似比的兩個相似三角形，寫出具體作法.（不必證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經過坐標原點
的兩條直線與橢圓
：
分別相交于點
、
和點
、
，其中直線
經過的左焦點
，直線
經過的右焦點
.當直線不垂直于坐標軸時，與
的斜率乘積為
.
（1）求橢圓的方程；
（2）求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】矩陣乘法運算
的幾何意義為平面上的點
在矩陣
的作用下變換成點
，記
，且
.
（1）若平面上的點
在矩陣
的作用下變換成點
，求點的坐標；
（2）若平面上相異的兩點、
在矩陣
的作用下，分別變換為點
、
，求證：若點
為線段
上的點，則點在的作用下的點
在線段
上；
（3）已知△
的頂點坐標為
、
、
，且△在矩陣
作用下變換成△
，記△與△的面積分別為
與
，求的值，并寫出一般情況（三角形形狀一般化且變換矩陣一般化）下與的關系（不要求證明）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學2018年的高考考生人數是2015年高考考生人數的
倍，為了更好地對比該校考生的升學情況，統計了該校2015年和2018年的高考情況，得到如圖柱狀圖：
則下列結論正確的是
A. 與2015年相比，2018年一本達線人數減少
B. 與2015年相比，2018年二本達線人數增加了
倍
C. 2015年與2018年藝體達線人數相同
D. 與2015年相比，2018年不上線的人數有所增加
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
，圓
.
（Ⅰ）
是拋物線
的焦點，
是拋物線上的定點，
，求拋物線的方程；
（Ⅱ）在（Ⅰ）的條件下，過點的直線
與圓
相切，設直線交拋物線于
，
兩點，則在
軸上是否存在點
使
？若存在，求出點的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，智能手機的更新換代極其頻繁和快速，而青少年對新事物的追求更是強烈，為了調查大學生更換手機的時間，現對某大學中的大學生使用一部手機的年限進行了問卷調查，并從參與調查的大學生中抽取了男生、女生各
人進行抽樣分析，制成如下的頻率分布直方圖.
（1）根據頻率分布直方圖，估計男大學生使用手機年限的中位數和女大學生使用手機年限的眾數；
（2）根據頻率分布直方圖，求出男大學生和女大學生使用手機年限的平均值，并分析比較男大學生和女大學生哪個群體更換手機的頻率更高.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
