
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若函數![]() 在
在![]() 有兩個零點,求m的取值范圍.
有兩個零點,求m的取值范圍.
【答案】(1)答案不唯一,具體見解析(2)![]()
【解析】
(1)首先求出函數的導函數因式分解為![]() ,再對參數
,再對參數![]() 分類討論可得;
分類討論可得;
(2)依題意可得![]() ,當
,當![]() 函數在定義域上單調遞增,不滿足條件;
函數在定義域上單調遞增,不滿足條件;
當![]() 時,由(1)得
時,由(1)得![]() 在
在![]() 為增函數,因為
為增函數,因為![]() ,
,![]() .再對
.再對![]() ,
,![]() ,
,![]() 三種情況討論可得.
三種情況討論可得.
解:(1)因為![]() ,所以
,所以![]() ,
,
即![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
①當![]() 時,
時,![]() ,當且僅當
,當且僅當![]() 時,等號成立.
時,等號成立.
故![]() 在
在![]() 為增函數.
為增函數.
②當![]() 時,
時,![]() ,
,
由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() ,
,![]() 為增函數,在
為增函數,在![]() 為減函數.
為減函數.
③當![]() 時,
時,![]() ,
,
由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() ,
,![]() 為增函數,在
為增函數,在![]() 為減函數.
為減函數.
綜上,當![]() 時,
時,![]() 在為
在為![]() 增函數;
增函數;
當![]() 時,
時,![]() 在
在![]() ,
,![]() 為增函數,在
為增函數,在![]() 為減函數;
為減函數;
當![]() 時,
時,![]() 在
在![]() ,
,![]() 為增函數,在
為增函數,在![]() 為減函數.
為減函數.
(2)因為![]() ,所以
,所以![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 為增函數,所以
為增函數,所以![]() 在
在![]() 至多一個零點.
至多一個零點.
②當![]() 時,由(1)得
時,由(1)得![]() 在
在![]() 為增函數.
為增函數.
因為![]() ,
,![]() .
.
(ⅰ)當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,![]() 時,
時,![]() ;
;
所以![]() 在
在![]() 為減函數,在
為減函數,在![]() 為增函數,
為增函數,![]() .
.
故![]() 在
在![]() 有且只有一個零點.
有且只有一個零點.
(ⅱ)當![]() 時,
時,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,
且![]() 在
在![]() 為減函數,在
為減函數,在![]() 為增函數.
為增函數.
所以![]() ,又
,又![]() ,
,
根據零點存在性定理,![]() 在
在![]() 有且只有一個零點.
有且只有一個零點.
又![]() 在
在![]() 上有且只有一個零點0.
上有且只有一個零點0.
故當![]() 時,
時,![]() 在
在![]() 有兩個零點.
有兩個零點.
(ⅲ)當![]() 時,
時,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,
且![]() 在
在![]() 為減函數,在
為減函數,在![]() 為增函數.
為增函數.
因為![]() 在
在![]() 有且只有一個零點0,
有且只有一個零點0,
若![]() 在
在![]() 有兩個零點,則
有兩個零點,則![]() 在
在![]() 有且只有一個零點.
有且只有一個零點.
又![]() ,所以
,所以![]() 即
即![]() ,所以
,所以![]() ,
,
即當![]() 時
時![]() 在
在![]() 有兩個零點.
有兩個零點.
綜上,m的取值范圍為![]()


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某地某月1日至15日的日平均溫度變化的折線圖,根據該折線圖,下列結論正確的是( )
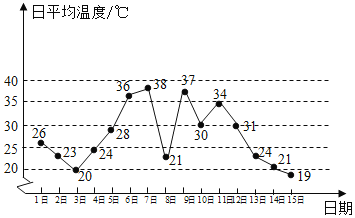
A. 這15天日平均溫度的極差為![]()
B. 連續三天日平均溫度的方差最大的是7日,8日,9日三天
C. 由折線圖能預測16日溫度要低于![]()
D. 由折線圖能預測本月溫度小于![]() 的天數少于溫度大于
的天數少于溫度大于![]() 的天數
的天數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】依照某發展中國家2018年的官方資料,將該國所有家庭按年收入從低到高的順序平均分為五組,依次為第一組至第五組,各組家庭的年收入總和占該國全部家庭的年收入總和的百分比如圖所示.
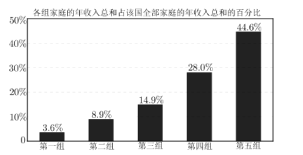
以下關于該國2018年家庭收入的判斷,一定正確的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入為全部家庭平均年收入的
的家庭平均年收入為全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
D. 收入最低的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若![]() 的值域為
的值域為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在這祥的實數
,是否存在這祥的實數![]() ,使函數
,使函數![]() 在區間
在區間![]() 內有且只有一個零點.若存在,求出
內有且只有一個零點.若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
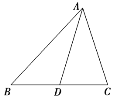
(1)求A;
(2)若AD為BC邊上的中線,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年遼寧省正式實施高考改革.新高考模式下,學生將根據自己的興趣、愛好、學科特長和高校提供的“選考科目要求”進行選課.這樣學生既能尊重自己愛好、特長做好生涯規劃,又能發揮學科優勢,進而在高考中獲得更好的成績和實現自己的理想.考改實施后,學生將在高二年級將面臨著![]() 的選課模式,其中“3”是指語、數、外三科必學內容,“1”是指在物理和歷史中選擇一科學習,“2”是指在化學、生物、地理、政治四科中任選兩科學習.某校為了更好的了解學生對“1”的選課情況,學校抽取了部分學生對選課意愿進行調查,依據調查結果制作出如下兩個等高堆積條形圖:根據這兩幅圖中的信息,下列哪個統計結論是不正確的( )
的選課模式,其中“3”是指語、數、外三科必學內容,“1”是指在物理和歷史中選擇一科學習,“2”是指在化學、生物、地理、政治四科中任選兩科學習.某校為了更好的了解學生對“1”的選課情況,學校抽取了部分學生對選課意愿進行調查,依據調查結果制作出如下兩個等高堆積條形圖:根據這兩幅圖中的信息,下列哪個統計結論是不正確的( )
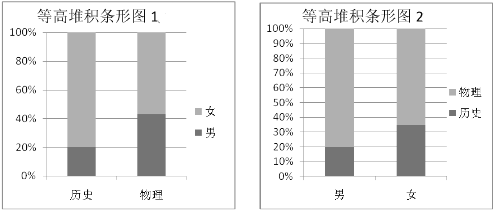
A.樣本中的女生數量多于男生數量
B.樣本中有學物理意愿的學生數量多于有學歷史意愿的學生數量
C.樣本中的男生偏愛物理
D.樣本中的女生偏愛歷史
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com