
如圖,設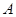 是棱長為
是棱長為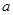 的正方體的一個頂點,過從此頂點出發的三條棱的中點作截面,對正方體的所有頂點都如此操作,所得的各截面與正方體各面共同圍成一個多面體,則關于此多面體有以下結論:①有
的正方體的一個頂點,過從此頂點出發的三條棱的中點作截面,對正方體的所有頂點都如此操作,所得的各截面與正方體各面共同圍成一個多面體,則關于此多面體有以下結論:①有 個頂點;②有
個頂點;②有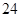 條棱;③有
條棱;③有 個面;④表面積為
個面;④表面積為 ;⑤體積為
;⑤體積為 .其中正確的結論是____________.(要求填上所有正確結論的序號)
.其中正確的結論是____________.(要求填上所有正確結論的序號)
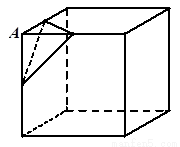
①②⑤
【解析】解:如圖,
原來的六個面還在只不過是變成了一個小正方形,再添了八個頂點各對應的一個三角形的面,所以總計6+8=14個面,故③錯;
每個正方形4條邊,每個三角形3條邊,4×6+3×8=48,考慮到每條邊對應兩個面,所以實際只有 ×48=24條棱.②正確;
×48=24條棱.②正確;
所有的頂點都出現在原來正方體的棱的中點位置,
原來的棱的數目是12,所以現在的頂點的數目是12.
或者從圖片上可以看出每個頂點對應4條棱,每條棱很明顯對應兩個頂點,所以頂點數是棱數的一半即12個.①正確;
三角形和四邊形的邊長都是 a,所以正方形總面積為6×
a,所以正方形總面積為6× ×a2=3a2,三角形總面積為8×
×a2=3a2,三角形總面積為8× ×
× a2sin60°=
a2sin60°= a2,表面積(3+
a2,表面積(3+ )a2,故④錯;
)a2,故④錯;
體積為原正方形體積減去8個三棱錐體積,每個三棱錐體積為8× (
( )3=
)3= a2,剩余總體積為a3-
a2,剩余總體積為a3- a3=
a3= a3⑤正確.
a3⑤正確.
故答案為:①②⑤.


科目:高中數學 來源: 題型:
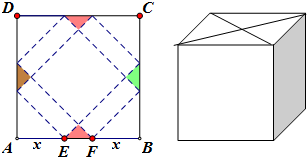 請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上,是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=x(cm).
請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上,是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=x(cm).查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
(04年上海卷)(16分)
如圖,P-ABC是底面邊長為1的正三棱錐,D、E、F分別為棱長PA、PB、PC上的點, 截面DEF∥底面ABC, 且棱臺DEF-ABC與棱錐P-ABC的棱長和相等.(棱長和是指多面體中所有棱的長度之和)
(1) 證明:P-ABC為正四面體;
(2) 若PD=![]() PA, 求二面角D-BC-A的大小;(結果用反三角函數值表示)
PA, 求二面角D-BC-A的大小;(結果用反三角函數值表示)
(3) 設棱臺DEF-ABC的體積為V, 是否存在體積為V且各棱長均相等的直
平行六面體,使得它與棱臺DEF-ABC有相同的棱長和? 若存在,請具體構造
出這樣的一個直平行六面體,并給出證明;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
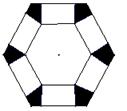
如圖,把邊長為![]() 的正六邊形紙板剪去相同的六個角,做成一個底面為正六邊形的無蓋六棱柱盒子,設高為
的正六邊形紙板剪去相同的六個角,做成一個底面為正六邊形的無蓋六棱柱盒子,設高為![]() ,所做成的盒子體積為
,所做成的盒子體積為![]() (不計接縫)。
(不計接縫)。
(1)寫出體積![]() 與高
與高![]() 的函數關系式;(2)當
的函數關系式;(2)當![]() 為多少時,體積
為多少時,體積![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省泰州市泰興三中高二(上)期中數學試卷(解析版) 題型:解答題
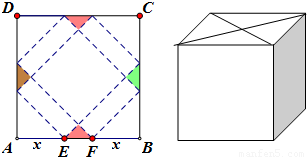 請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上,是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=x(cm).
請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上,是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=x(cm).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com