若數列{an}滿足
＝d(n∈N*，d為常數)，則稱數列{an}為“調和數列”．已知正項數列
為“調和數列”，且b1＋b2＋…＋b9＝90，則b4·b6的最大值是 ( )．
A．10 B．100 C．200 D．400
陽光課堂同步練習系列答案科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-6-3練習卷（解析版） 題型：填空題
已知橢圓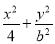
＝1(0<b<2)與y軸交于A，B兩點，點F為該橢圓的一個焦點，則△ABF面積的最大值為________．
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-5-2練習卷（解析版） 題型：解答題
如圖，在三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.
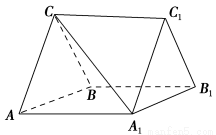
(1)證明：AB⊥A1C；
(2)若AB＝CB＝2，A1C＝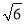
，求三棱柱ABC－A1B1C1的體積；
(3)若平面ABC⊥平面AA1B1B，AB＝CB＝2，求直線A1C與平面BB1C1C所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-5-1練習卷（解析版） 題型：選擇題
某幾何體的三視圖如圖所示，則該幾何體的體積為( )．
A．16＋8π B．8＋8π C．16＋16π D．8＋16π
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-4-2練習卷（解析版） 題型：解答題
在等差數列{an}中，a3＋a4＋a5＝84，a9＝73.
(1)求數列{an}的通項公式；
(2)對任意m∈N*，將數列{an}中落入區間(9m,92m)內的項的個數記為bm，求數列{bm}的前m項和Sm.
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-4-1練習卷（解析版） 題型：解答題
設{an}是公比大于1的等比數列，Sn為數列{an}的前n項和．已知S3＝7，且a1＋3,3a2，a3＋4構成等差數列．
(1)求數列{an}的通項公式；
(2)令bn＝ln a3n＋1，n＝1,2，…，求數列{bn}的前n項和Tn.
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-4-1練習卷（解析版） 題型：選擇題
已知{an}為等比數列，下面結論中正確的是( )．
A．a1＋a3≥2a2 B．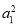
＋
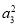≥2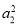
C．若a1＝a3，則a1＝a2 D．若a3>a1，則a4>a2
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-3-1練習卷（解析版） 題型：填空題
函數y＝tan ωx(ω＞0)與直線y＝a相交于A，B兩點，且|AB|最小值為π，則函數f(x)＝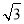
sin ωx－cos ωx的單調增區間是________．
查看答案和解析>>
科目：高中數學 來源：2014年高考數學（理）二輪專題復習知能提升演練1-1-3練習卷（解析版） 題型：解答題
為了在夏季降溫和冬季供暖時減少能源損耗，房屋的屋頂和外墻需要建造隔熱層，某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元，該建筑物每年的能源消耗費用C(單位：萬元)與隔熱層厚度x(單位：cm)滿足關系：C(x)＝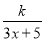
(0≤x≤10)，若不建隔熱層，每年能源消耗費用為8萬元．設f(x)為隔熱層建造費用與20年的能源消耗費用之和．
(1)求k的值及f(x)的表達式；
(2)隔熱層修建多厚時，總費用f(x)達到最小，并求最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
