
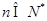 時,
時,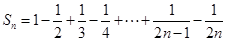 ,
,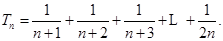
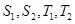 ;
;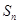 與
與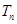 的關(guān)系,并用數(shù)學(xué)歸納法證明.
的關(guān)系,并用數(shù)學(xué)歸納法證明.科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
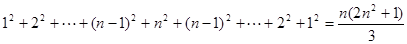 時,由
時,由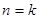 的假設(shè)到證明
的假設(shè)到證明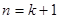 時,等式左邊應(yīng)添加的式子是( )
時,等式左邊應(yīng)添加的式子是( )A.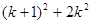 | B.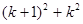 | C.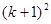 | D.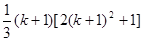 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
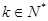 )時,命題成立,則可以推出n=k+1時,該命題也成立.現(xiàn)已知n=6時命題不成立( ).
)時,命題成立,則可以推出n=k+1時,該命題也成立.現(xiàn)已知n=6時命題不成立( ).| A.當(dāng)n=5時命題不成立 | B.當(dāng)n=7時命題不成立 |
| C.當(dāng)n=5時命題成立 | D.當(dāng)n=8時命題成立 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
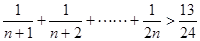 時,由k到k+1,不等式左端的變化是( )
時,由k到k+1,不等式左端的變化是( )A.增加 項 項 | B.增加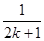 和 和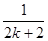 兩項 兩項 |
C.增加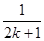 和 和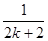 兩項且減少 兩項且減少 一項 一項 | D.以上結(jié)論均錯 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
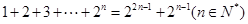 ,第二步,“假設(shè)當(dāng)
,第二步,“假設(shè)當(dāng)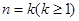 時等式成立,則當(dāng)
時等式成立,則當(dāng)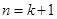 時有
時有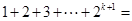
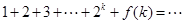 ”,其中
”,其中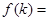 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
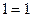 ,
,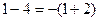 ,
,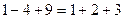 ,
,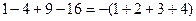 ,則第5個等式為 ,…,推廣到第
,則第5個等式為 ,…,推廣到第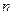 個等式為__ _;(注意:按規(guī)律寫出等式的形式,不要求計算結(jié)果.)
個等式為__ _;(注意:按規(guī)律寫出等式的形式,不要求計算結(jié)果.)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com