
函數f(x)=ln x-![]() 零點所在的大致區間是
零點所在的大致區間是
A.(1,2)
B.(2,3)
C.(1,![]() )和(3,4)
)和(3,4)
D.(e,+∞)
|
解析:用驗證法.從已知的區間(a,b)求f(a)、f(b),判斷是否有f(a)·(b)<0.∵f(1)=-2<0,f(2)=ln 2-1<0,∴在(1,2)內f(x)無零點,故排除A.∵f(3)= ln 3- |
|
確定零點所在區間,只要判斷區間[a,b]的端點值的乘積是否有f(a)f·(b)<0,并且看函數y=f(x)在[a,b]上是否是連續曲線.這里說“若f(a)·f(b)<0,則在區間(a,b)內方程f(x)=0至少有一個實數解”,指出了方程f(x)=0實數解的存在,并不能判斷具體有多少個實數解. |


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
設g(x)是函數f(x)=ln(x+1)+2x的導函數,若函數g(x)按向量a平移后得到函數y=![]() ,則向量a等于
,則向量a等于
A.(1,2) B.(-1,-2) C.(-2,-1) D.(2,1)
查看答案和解析>>
科目:高中數學 來源:2010年湖南省洞口四中下學期高二單元數學試題 題型:解答題
(本小題滿分12分)已知函數f(x)=ln(x+1)-x.
⑴求函數f(x)的單調遞減區間;
⑵若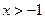 ,證明:
,證明: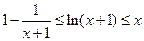 .
.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年內蒙古高三下學期綜合檢測(一)文科數學試卷(解析版) 題型:選擇題
函數f(x)=ln(4+3x-x2)的單調遞減區間是
A.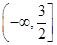 B.
B.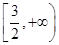 C.
C.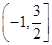 D.
D.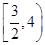
查看答案和解析>>
科目:高中數學 來源:2010-2011學年云南省高二下學期期末考試理科數學卷 題型:選擇題
已知函數f(x)=ln(x+1)- x2+x-m(m為常數)的圖象上P點處的切線與直線x-
x2+x-m(m為常數)的圖象上P點處的切線與直線x- y+2=0的夾角為45°,則點P的橫坐標為(
)
y+2=0的夾角為45°,則點P的橫坐標為(
)
A.
0 B.  C.
C.  D. ±
D. ±
查看答案和解析>>
科目:高中數學 來源:2010年湖南省下學期高二單元數學試題 題型:解答題
(本小題滿分12分)已知函數f(x)=ln(x+1)-x.
⑴求函數f(x)的單調遞減區間;
⑵若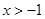 ,證明:
,證明: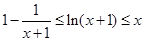 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com