
【題目】(本小題共13分)已知函數![]()
![]() 的最小正周期為
的最小正周期為![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函數![]() 的單調區間及其圖象的對稱軸方程.
的單調區間及其圖象的對稱軸方程.
【答案】解:(Ⅰ)![]() ………………………2分
………………………2分
![]() , …………………………3分
, …………………………3分
因為![]() 最小正周期為
最小正周期為![]() ,所以
,所以![]() ,解得
,解得![]() ,………………………4分
,………………………4分
所以![]() , …………………… 5分
, …………………… 5分
所以![]() . …………………………6分
. …………………………6分
(Ⅱ)分別由![]() ,
,![]()
可得![]() ,
,![]() ………8分
………8分
所以,函數![]() 的單調增區間為
的單調增區間為![]() ;
;
![]() 的單調減區間為
的單調減區間為![]() ………………………10分
………………………10分
由![]() 得
得![]() .
.
所以,![]() 圖象的對稱軸方程為
圖象的對稱軸方程為![]() . ………………………13分
. ………………………13分
【解析】
試題(Ⅰ)![]()
![]() ,因為
,因為![]() 最小正周期為
最小正周期為![]() ,可得
,可得![]() , 可得
, 可得![]() ,即可求出
,即可求出![]() .(Ⅱ)分別由
.(Ⅱ)分別由![]() ,
,![]() 即可求出單調區間;再根據
即可求出單調區間;再根據![]() ,可得
,可得
![]() 圖象的對稱軸方程.
圖象的對稱軸方程.
試題解析:解:(Ⅰ)![]()
![]() ,
,
因為![]() 最小正周期為
最小正周期為![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以![]() .
.
(Ⅱ)分別由![]() ,
,![]()
可得![]() ,
,![]()
所以,函數![]() 的單調增區間為
的單調增區間為![]() ;
;
![]() 的單調減區間為
的單調減區間為![]()
由![]() 得
得![]() .
.
所以,![]() 圖象的對稱軸方程為
圖象的對稱軸方程為![]() .
.


 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 右焦點F的坐標為
右焦點F的坐標為![]() ,點
,點![]() 在橢圓C上,過F且斜率為
在橢圓C上,過F且斜率為![]() 的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,O為坐標原點.
的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,O為坐標原點.
(I)求橢圓C的方程;
(Ⅱ)設線段AB的垂直平分線與x軸、y軸分別相交于點C,D.若![]() 與
與![]() 的面積相等,求直線l的斜率k.
的面積相等,求直線l的斜率k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省GDP情況圖,則下列陳述中不正確的是( )

A.2017年第一季度GDP增速由高到低排位第5的是浙江省
B.2017年第一季度GDP總量和增速由高到低排位均居同一位的省只有1個
C.去年同期河南省的GDP總量不超過4000億元
D.與去年同期相比,2017年第一季度五個省的GDP總量均實現了增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校![]() 名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共
名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共![]() 種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以
種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以![]() 人一組或者
人一組或者![]() 人一組.如果
人一組.如果![]() 人一組,則必須角色相同;如果
人一組,則必須角色相同;如果![]() 人一組,則
人一組,則![]() 人角色相同或者
人角色相同或者![]() 人為級別連續的
人為級別連續的![]() 個不同角色.已知這
個不同角色.已知這![]() 名學生扮演的角色有
名學生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,現在新加入
人,現在新加入![]() 名學生,將這
名學生,將這![]() 名學生分成
名學生分成![]() 組進行游戲,則新加入的學生可以扮演的角色的種數為________.
組進行游戲,則新加入的學生可以扮演的角色的種數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若從第二項起的每一項均大于該項之前的所有項的和,則稱
,若從第二項起的每一項均大于該項之前的所有項的和,則稱![]() 為
為![]() 數列.
數列.
(1)若![]() 的前
的前![]() 項和
項和![]() ,試判斷
,試判斷![]() 是否是
是否是![]() 數列,并說明理由;
數列,并說明理由;
(2)設數列![]() 是首項為
是首項為![]() 、公差為
、公差為![]() 的等差數列,若該數列是
的等差數列,若該數列是![]() 數列,求
數列,求![]() 的取值范圍;
的取值范圍;
(3)設無窮數列![]() 是首項為
是首項為![]() 、公比為
、公比為![]() 的等比數列,有窮數列
的等比數列,有窮數列![]() ,
,![]() 是從
是從![]() 中取出部分項按原來的順序所組成的不同數列,其所有項和分別為
中取出部分項按原來的順序所組成的不同數列,其所有項和分別為![]() ,
,![]() ,求
,求![]() 是
是![]() 數列時
數列時![]() 與
與![]() 所滿足的條件,并證明命題“若
所滿足的條件,并證明命題“若![]() 且
且![]() ,則
,則![]() 不是
不是![]() 數列”.
數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(多選題)下列說法中,正確的命題是( )
A.已知隨機變量![]() 服從正態分布
服從正態分布![]() ,
,![]() ,則
,則![]() .
.
B.以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和0.3.
和0.3.
C.已知兩個變量具有線性相關關系,其回歸直線方程為![]() ,若
,若![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
D.若樣本數據![]() ,
,![]() ,…,
,…,![]() 的方差為2,則數據
的方差為2,則數據![]() ,
,![]() ,…,
,…,![]() 的方差為16.
的方差為16.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系;曲線C1的普通方程為(x-1)2 +y2 =1,曲線C2的參數方程為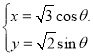 (θ為參數).
(θ為參數).
(Ⅰ)求曲線C1和C2的極坐標方程:
(Ⅱ)設射線θ=![]() (ρ>0)分別與曲線C1和C2相交于A,B兩點,求|AB|的值.
(ρ>0)分別與曲線C1和C2相交于A,B兩點,求|AB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com