
【題目】(2017·深圳二模)在“新零售”模式的背景下,某大型零售公司為推廣線下分店,計劃在S市的A區開設分店.為了確定在該區開設分店的個數,該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記x表示在各區開設分店的個數,y表示這x個分店的年收入之和.
x(個) | 2 | 3 | 4 | 5 | 6 |
y(百萬元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)該公司已經過初步判斷,可用線性回歸模型擬合y與x的關系,求y關于x的線性回歸方程;
(2)假設該公司在A區獲得的總年利潤z(單位:百萬元)與x,y之間的關系為z=y-0.05x2-1.4,請結合(1)中的線性回歸方程,估算該公司應在A區開設多少個分店時,才能使A區平均每個分店的年利潤最大?
參考公式: 
【答案】(1)![]() =0.85x+0.6.(2)開設4個分店
=0.85x+0.6.(2)開設4個分店
【解析】
試題
(1)由題中所給數據及公式可得線性回歸方程為![]() .(2)設該區每個分店的平均利潤為t,由(1)可得t的預測值
.(2)設該區每個分店的平均利潤為t,由(1)可得t的預測值![]() 與x之間的關系為
與x之間的關系為![]() ,
,
由基本不等式可得x=4時![]() 有最大值,故可估算開設4個分店才能使A區的每個分店的平均年利潤最大.
有最大值,故可估算開設4個分店才能使A區的每個分店的平均年利潤最大.
試題解析:
(1)法一:由表中數據和參考數據得,
![]() =4,
=4,![]() =4,
=4, ![]() (xi-
(xi-![]() )2=10,
)2=10,![]() (xi-
(xi-![]() )(yi-
)(yi-![]() )=5,
)=5,
∴![]() =
=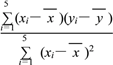 =
=![]() =0.85,
=0.85,
∴![]() =
=![]() -
-![]()
![]() =4-4×0.85=0.6,
=4-4×0.85=0.6,
∴線性回歸方程![]() =0.85x+0.6.
=0.85x+0.6.
法二:由表中數據和參考數據得,
![]() =4,
=4,![]() =4,
=4, ![]() xiyi=88.5,
xiyi=88.5,![]() x=90,
x=90,
∴![]() =
=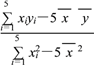 =
=![]() =0.85,
=0.85,
∴![]() =
=![]() -
-![]()
![]() =4-4×0.85=0.6,
=4-4×0.85=0.6,
∴線性回歸方程![]() =0.85x+0.6.
=0.85x+0.6.
(2)由題意,可知總年利潤z的預測值![]() 與x之間的關系為
與x之間的關系為![]() =-0.05x2+0.85x-0.8,
=-0.05x2+0.85x-0.8,
設該區每個分店的平均利潤為t,則![]() ,
,
∴t的預測值![]() 與x之間的關系為
與x之間的關系為
![]() =-0.05x-
=-0.05x-![]() +0.85=-0.01
+0.85=-0.01![]() +0.85≥-0.01×2
+0.85≥-0.01×2![]() +0.85=0.45,
+0.85=0.45,
當且僅當5x=![]() ,即x=4時,
,即x=4時,![]() 取到最大值,
取到最大值,
∴該公司在A區開設4個分店時,才能使A區的每個分店的平均年利潤最大.


科目:高中數學 來源: 題型:
【題目】保險公司統計的資料表明:居民住宅區到最近消防站的距離x(單位:千米)和火災所造成的損失數額y(單位:千元)有如下的統計資料:
距消防站距離x(千米) | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
火災損失費用y(千元) | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明y與x有線性相關關系,試求:
(Ⅰ)求相關系數![]() (精確到0.01);
(精確到0.01);
(Ⅱ)求線性回歸方程(精確到0.01);
(III)若發生火災的某居民區與最近的消防站相距10.0千米,評估一下火災的損失(精確到0.01).
參考數據:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
參考公式:相關系數  ,回歸方程
,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形.點
是正方形.點![]() 是棱
是棱![]() 的中點,平面
的中點,平面![]() 與棱
與棱![]() 交于點
交于點![]() .
.

(1)求證:![]() ;
;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,試證明
,試證明![]() 平面
平面![]() ;
;
(3)在(2)的條件下,線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]()
![]() 平面
平面![]() ?(直接給出結論,不需要說明理由)
?(直接給出結論,不需要說明理由)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高中生在被問及“家,朋友聚集的地方,個人空間”三個場所中“感到最幸福的場所在哪里?”這個問題時,從中國某城市的高中生中,隨機抽取了55人,從美國某城市的高中生中隨機抽取了45人進行答題.中國高中生答題情況是:選擇家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、個人空間占
、個人空間占![]() .美國高中生答題情況是:朋友聚集的地方占
.美國高中生答題情況是:朋友聚集的地方占![]() 、家占
、家占![]() 、個人空間占
、個人空間占![]() .如下表:
.如下表:
在家里最幸福 | 在其它場所幸福 | 合計 | |
中國高中生 | |||
美國高中生 | |||
合計 |
(Ⅰ)請將![]() 列聯表補充完整;試判斷能否有
列聯表補充完整;試判斷能否有![]() 的把握認為“戀家”與否與國別有關;
的把握認為“戀家”與否與國別有關;
(Ⅱ)從被調查的不“戀家”的美國學生中,用分層抽樣的方法選出4人接受進一步調查,再從4人中隨機抽取2人到中國交流學習,求2人中含有在“個人空間”感到幸福的學生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() …是然對數底數.
…是然對數底數.
(1)若函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
, ![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求使不等式
時,求使不等式![]() 在一切實數上恒成立的最大正整數
在一切實數上恒成立的最大正整數![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若對任意![]() ,
, ![]() 有唯一確定的
有唯一確定的![]() 與之對應,則稱
與之對應,則稱![]() 為關于
為關于![]() ,
, ![]() 的二元函數,現定義滿足下列性質的
的二元函數,現定義滿足下列性質的![]() 為關于實數
為關于實數![]() ,
, ![]() 的廣義“距離”.
的廣義“距離”.
(![]() )非負性:
)非負性: ![]() ,當且僅當
,當且僅當![]() 時取等號;
時取等號;
(![]() )對稱性:
)對稱性: ![]() ;
;
(![]() )三角形不等式:
)三角形不等式: ![]() 對任意的實數
對任意的實數![]() 均成立.
均成立.
給出三個二元函數:①![]() ;②
;②![]() ;③
;③![]() ,
,
則所有能夠成為關于![]() ,
, ![]() 的廣義“距離”的序號為__________.
的廣義“距離”的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱.某市為了了解人們對“一帶一路”的認知程度,對不同年齡和不同職業的人舉辦了一次“一帶一路”知識競賽,滿分100分(90分及以上為認知程度高).現從參賽者中抽取了![]() 人,按年齡分成5組,第一組:
人,按年齡分成5組,第一組: ![]() ,第二組:
,第二組: ![]() ,第三組:
,第三組: ![]() ,第四組:
,第四組: ![]() ,第五組:
,第五組: ![]() ,得到如圖所示的頻率分布直方圖,已知第一組有6人.
,得到如圖所示的頻率分布直方圖,已知第一組有6人.
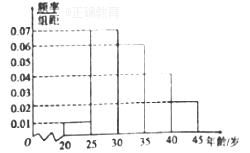
(1)求![]() ;
;
(2)求抽取的![]() 人的年齡的中位數(結果保留整數);
人的年齡的中位數(結果保留整數);
(3)從該市大學生、軍人、醫務人員、工人、個體戶 五種人中用分層抽樣的方法依次抽取6人,42人,36人,24人,12人,分別記為1~5組,從這5個按年齡分的組和5個按職業分的組中每組各選派1人參加知識競賽,分別代表相應組的成績,年齡組中1~5組的成績分別為93,96,97,94,90,職業組中1~5組的成績分別為93,98,94,95,90.
(Ⅰ)分別求5個年齡組和5個職業組成績的平均數和方差;
(Ⅱ)以上述數據為依據,評價5個年齡組和5個職業組對“一帶一路”的認知程度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com