
【題目】已知函數f1(x)=![]() x2,f2(x)=alnx(其中a>0).
x2,f2(x)=alnx(其中a>0).
(1)求函數f(x)=f1(x)·f2(x)的極值;
(2)若函數g(x)=f1(x)-f2(x)+(a-1)x在區間(![]() ,e)內有兩個零點,求正實數a的取值范圍;
,e)內有兩個零點,求正實數a的取值范圍;
(3)求證:當x>0時,![]() .(說明:e是自然對數的底數,e=2.71828…)
.(說明:e是自然對數的底數,e=2.71828…)
【答案】(1) 函數f(x)的極小值為![]() ,無極大值.
,無極大值.
(2) ![]() .
.
(3)見解析.
【解析】分析:(1)求![]() ,求出方程
,求出方程![]() 的解
的解![]() ,確定
,確定![]() 兩側
兩側![]() 的正負,得極值;
的正負,得極值;
(2)求出![]() ,確定出
,確定出![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,結合零點存在定理可知
上遞增,結合零點存在定理可知![]() 在
在![]() 上有兩個零點的條件,得出
上有兩個零點的條件,得出![]() 的范圍;
的范圍;
(3)不等式可變形為![]() ,其中由(1)知
,其中由(1)知![]() 的最小值為
的最小值為![]() ,下面只要求得
,下面只要求得![]() 的最大值,證明此最大值
的最大值,證明此最大值![]() 即可.
即可.
詳解: (1)∵f(x)=f1(x)·f2(x)=![]() ax2·lnx,
ax2·lnx,
∴f ′(x)=axlnx+![]() ax=
ax=![]() ax(2lnx+1)(x>0,a>0),
ax(2lnx+1)(x>0,a>0),
由f ′(x)>0,得x>e-![]() ,由f ′(x)<0,得0<x<e-
,由f ′(x)<0,得0<x<e-![]() ,
,
故函數f(x)在(0,e-![]() )上單調遞減,在(e-
)上單調遞減,在(e-![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
所以函數f(x)的極小值為f(e-![]() )=-
)=-![]() ,無極大值.
,無極大值.
(2)函數g(x)=![]() x2-alnx+(a-1)x,
x2-alnx+(a-1)x,
則g′(x)=x-![]() +(a-1)=
+(a-1)=![]() =
=![]() ,
,
令g′(x)=0,∵a>0,解得x=1,或x=-a(舍去),
當0<x<1時,g′(x)<0,g(x)在(0,1)上單調遞減;
當x>1時,g′(x)>0,g(x)在(1,+∞)上單調遞增.
函數g(x)在區間(![]() ,e)內有兩個零點,
,e)內有兩個零點,
只需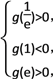 即
即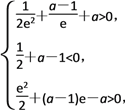 ∴
∴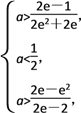
故實數a的取值范圍是(![]() ,
,![]() ).
).
(3)問題等價于x2lnx>![]() -
-![]() .由(1)知f(x)=x2lnx的最小值為-
.由(1)知f(x)=x2lnx的最小值為-![]() .
.
設h(x)=![]() -
-![]() ,h′(x)=-
,h′(x)=-![]() ,
,
易知h(x)在(0,2)上單調遞增,在(2,+∞)上單調遞減. 10分
∴h(x)max=h(2)=![]() -
-![]() ,∵-
,∵-![]() -(
-(![]() -
-![]() )=
)=![]() -
-![]() -
-![]() =
=![]() =
=![]() >0,
>0,
∴f(x)min>h(x)max,∴x2lnx>![]() -
-![]() ,故當x>0時,lnx+
,故當x>0時,lnx+![]() -
-![]() >0.
>0.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 為偶函數,且函數
為偶函數,且函數
![]() 圖象的兩相鄰對稱軸間的距離為
圖象的兩相鄰對稱軸間的距離為![]() .
.
(1)求![]() 的值;
的值;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后,再將得到的圖象上各點的橫坐標伸長到原來的
個單位后,再將得到的圖象上各點的橫坐標伸長到原來的![]() 倍,縱坐標不變,得到函數
倍,縱坐標不變,得到函數![]() 的圖象,求
的圖象,求![]() 的單調遞減區間.
的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2019·武漢六中]袋子中有四個小球,分別寫有“武、漢、軍、運”四個字,從中任取一個小球,有放回抽取,直到取到“軍”“運”二字就停止,用隨機模擬的方法估計恰好在第三次停止的概率:利用電腦隨機產生0到3之間取整數值的隨機數,分別用0,1,2,3代表“軍、運、武、漢”這四個字,以每三個隨機數為一組,表示取球三次的結果,經隨機模擬產生了以下16組隨機數:
232 321 230 023 123 021 132 220
231 130 133 231 331 320 122 233
由此可以估計,恰好第三次就停止的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2019·牡丹江一中]某校從參加高一年級期末考試的學生中抽取60名學生的成績(均為整數),其成績的頻率分布直方圖如圖所示,由此估計此次考試成績的中位數,眾數和平均數分別是( )
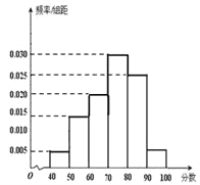
A. 73.3,75,72 B. 73.3,80,73
C. 70,70,76 D. 70,75,75
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
, ![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學只有兩位說的話是對的,則獲得一等獎的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函數h(x)=f(x)﹣g(x)在(0,+∞)上單調遞增,求實數a的取值范圍;
(2)若直線g(x)=ax+b是函數f(x)=lnx﹣ ![]() 圖象的切線,求a+b的最小值;
圖象的切線,求a+b的最小值;
(3)當b=0時,若f(x)與g(x)的圖象有兩個交點A(x1 , y1),B(x2 , y2),求證:x1x2>2e2 . (取e為2.8,取ln2為0.7,取 ![]() 為1.4)
為1.4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在R上的奇函數,且x≥0時有
是定義在R上的奇函數,且x≥0時有![]() .
.
(1)寫出函數![]() 的單調區間(不要證明);
的單調區間(不要證明);
(2)解不等式![]() ;
;
(3)求函數![]() 在[﹣m,m]上的最大值和最小值.
在[﹣m,m]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}的前n項和為Sn , 且Sn=3﹣ ![]() an , bn是an與an+1的等差中項,則數列{bn}的通項公式為( )
an , bn是an與an+1的等差中項,則數列{bn}的通項公式為( )
A.4×3n
B.4×( ![]() )n
)n
C.![]() ×(
×( ![]() )n﹣1
)n﹣1
D.![]() ×(
×( ![]() )n
)n
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com