
【題目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)當x∈[0, ![]() ]時,求|
]時,求| ![]() +
+ ![]() |的取值范圍;
|的取值范圍;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求當k為何值時,g(x)的最小值為﹣
,求當k為何值時,g(x)的最小值為﹣ ![]() .
.
【答案】
(1)解: ![]() =(sinx﹣2cosx,sinx),
=(sinx﹣2cosx,sinx),
| ![]() |2=(sinx﹣2cosx,sinx)2
|2=(sinx﹣2cosx,sinx)2
=2sin2x﹣4sinxcosx+4cos2x
=2cos2x﹣4sinxcosx+2
=cos2x﹣2sin2x+3
= ![]() cos(2x+φ)+3,其中,tanφ=2,
cos(2x+φ)+3,其中,tanφ=2,
又∵x∈[0, ![]() ],
],
∴ ![]() ,
,
∴ ![]() 在
在 ![]() 上單調遞減,
上單調遞減,
∴| ![]() cos(2x+φ)|2∈[1,4],
cos(2x+φ)|2∈[1,4],
∴| ![]() +
+ ![]() |∈[1,2].
|∈[1,2].
(2)解: ![]() =(2sinx,cosx+k),
=(2sinx,cosx+k),
g(x)=( ![]() )
) ![]()
=﹣4sinxcosx+(cosx+k)(sinx﹣k)
=﹣3sinxcosx+k(sinx﹣cosx)﹣k2
令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),
),
則t∈[﹣ ![]() ,
, ![]() ],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
所以 ![]() .
.
所以g(x)可化為 ![]() ,
,
對稱軸  .
.
①當 ![]() ,即
,即 ![]() 時,
時, ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
所以 ![]() .
.
因為 ![]() ,
,
所以此時無解.
②當 ![]() ,即
,即 ![]() 時,
時, ![]() .
.
由﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,得k=0∈[﹣3
,得k=0∈[﹣3 ![]() ,3
,3 ![]() ].
].
③當﹣ ![]() ,即k<﹣3
,即k<﹣3 ![]() 時,
時,
g(x)min=h( ![]() )=﹣k2+
)=﹣k2+ ![]() k+
k+ ![]() ,
,
由﹣k2+ ![]() k+
k+ ![]() =﹣
=﹣ ![]() ,得k2﹣
,得k2﹣ ![]() k﹣3=0,
k﹣3=0,
所以k= ![]() .
.
因為k ![]() ,所以此時無解.
,所以此時無解.
綜上所述,當k=0時,g(x)的最小值為﹣ ![]() .
.
【解析】(1)由已知利用平面向量的坐標運算可得 ![]() =(sinx﹣2cosx,sinx),利用三角函數恒等變換的應用可得|
=(sinx﹣2cosx,sinx),利用三角函數恒等變換的應用可得| ![]() |2=
|2= ![]() cos(2x+φ)+3,其中,tanφ=2,又x∈[0,
cos(2x+φ)+3,其中,tanφ=2,又x∈[0, ![]() ],可求
],可求 ![]() ,利用余弦函數的單調性即可得解|
,利用余弦函數的單調性即可得解| ![]() +
+ ![]() |的取值范圍;(2)利用平面向量數量積的運算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2,令t=sinx﹣cosx=
|的取值范圍;(2)利用平面向量數量積的運算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2,令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),則g(x)可化為
),則g(x)可化為 ![]() ,對稱軸
,對稱軸 ![]() .利用二次函數的圖象和性質分類討論即可得解.
.利用二次函數的圖象和性質分類討論即可得解.
【考點精析】利用平面向量的坐標運算對題目進行判斷即可得到答案,需要熟知坐標運算:設![]() ,
,![]() 則
則![]() ;
;![]() ;設
;設![]() ,則
,則![]() .
.


科目:高中數學 來源: 題型:
【題目】已知三棱柱ABC﹣A1B1C1的側棱與底面垂直,體積為 ![]() ,底面是邊長為
,底面是邊長為 ![]() 的正三角形.若P為底面A1B1C1的中心,則PA與平面ABC所成角的大小為( )
的正三角形.若P為底面A1B1C1的中心,則PA與平面ABC所成角的大小為( )
A.120°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若正整數N除以正整數m后的余數為n,則記為N≡n(bmodm),例如10≡2(bmod4).下面程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執行該程序框圖,則輸出的i等于( ) 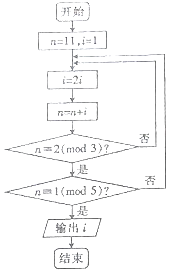
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= 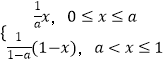 ,a為常數,且a∈(0,1).
,a為常數,且a∈(0,1).
(1)若x0滿足f(x0)=x0 , 則稱x0為f(x)的一階周期點,證明函數f(x)有且只有兩個一階周期點;
(2)若x0滿足f(f(x0))=x0 , 且f(x0)≠x0 , 則稱x0為f(x)的二階周期點,當a= ![]() 時,求函數f(x)的二階周期點.
時,求函數f(x)的二階周期點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的偶函數f(x),滿足f(x+1)=f(x﹣1),且f(x)在[﹣3,﹣2]上是增函數,又α、β是銳角三角形的兩個內角,則( )
A.f(sinα)>f(cosβ)
B.f(cosα)<f(cosβ)
C.f(sinα)<f(cosβ)
D.f(sinα)<f(sinβ)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C的對邊分別是a,b,c,且A、B、C成等差數列
(1)若 ![]() ,求△ABC的面積
,求△ABC的面積
(2)若sinA、sinB、sinC成等比數列,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正三棱柱ABC﹣A1B1C1的各個棱長都相等,E為BC的中點,動點F在CC1上,且不與點C重合
(1)當CC1=4CF時,求證:EF⊥A1C
(2)設二面角C﹣AF﹣E的大小為α,求tanα的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到函數y=sin ![]() 的圖象,只需把函數y=sin3x的圖象上所有的點( )
的圖象,只需把函數y=sin3x的圖象上所有的點( )
A.向左平移 ![]() 個單位長度
個單位長度
B.向左平移 ![]() 個單位長度
個單位長度
C.向右平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com