
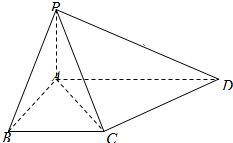
 如圖,四棱錐P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD為直角梯形,∠ABC=∠BAD=90°,PA=BC=$\frac{1}{2}$AD.
如圖,四棱錐P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD為直角梯形,∠ABC=∠BAD=90°,PA=BC=$\frac{1}{2}$AD.分析 (1)設PA=1,由勾股定理逆定理得AC⊥CD,根據線面垂直的性質可知PA⊥CD,又PA∩AC=A,根據線面垂直的判定定理可知CD⊥面PAC,
(2)在棱PD上存在一點E,E為PD中點,使CE∥平面PAB,取AD的中點為F.連接EF,CF.由題設條件推導出EF∥PA,CF∥AB,得到面EFC∥面PAB,由此能夠證明CE∥面PAB.
解答 解:(1)證明:設PA=1.
由題意PA=BC=1,AD=2.
∵AB=1,BC=$\frac{1}{2}$,由∠ABC=∠BAD=90°.易得CD=AC=$\sqrt{2}$.
由勾股定理逆定理得AC⊥CD.
又∵PA⊥面ABCD,CD?面ABCD,
∴PA⊥CD.又PA∩AC=A,∴CD⊥面PAC.
(2)在棱PD上存在一點E,E為PD中點,使CE∥平面PAB
理由:取AD的中點F.連接EF,CF.
∵PA⊥面ABCD.底面ABCD為直角梯形,∠ABC=∠BAD=90°,BC=$\frac{1}{2}$AD,E為PD的中點.
∴EF∥PA,CF∥AB,
∴面EFC∥面PAB,
所以CE∥面PAB.∴棱PD上存在一點E,E為PD中點,使CE∥平面PAB.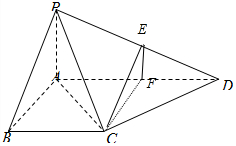
點評 本小題主要考查空間中的線面關系,考查線面平行、面面垂直的判定,考查空間想象能力和推理論證能力,考查轉化思想,屬于中檔題.


 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com