考點:橢圓的簡單性質
專題:計算題,解三角形,圓錐曲線的定義、性質與方程
分析:(1)運用橢圓的定義和余弦定理及面積公式,即可求得;
(2)設p(x,y),根據橢圓方程求得兩焦點坐標,根據∠F1PF2是鈍角推斷出PF12+PF22<F1F22代入p坐標求得x和y的不等式關系,求得x的范圍.
解答:
(1)解:∵橢圓的方程為
+y
2=1,
∴a=2,b=1,c=
.
又∵P為橢圓上一點,∠F
1PF
2=60°,F
1、F
2為左右焦點,
∴|F
1P|+|PF
2|=2a=4,|F
1F
2|=2
,
∴|F
1F
2|
2=(|PF
1|+|PF
2|)
2-2|F
1P||PF
2|-2|F
1P|•|PF
2|cos60°
=16-3|F
1P|•|PF
2|=12,
∴|F
1P|•|PF
2|=
.
∴S△PF
1F
2=
|F
1P|•|PF
2|sin60°
=
×
×
=
;
(2)設p(x,y),則 F
1(-
,0),F
2(
,0),
且∠F
1PF
2是鈍角,PF
12+PF
22<F
1F
22即(x
+)
2+y
2+(x-
)
2+y
2<12,
?x
2+3+y
2<6,即x
2+(1-
)<3即x
2<
.即-
<x<
.
故點P的橫坐標的取值范圍(-
,
).
點評:本題主要考查了橢圓的定義和方程及簡單性質和解不等式,考查余弦定理和面積公式的運用,考查運算能力,屬于中檔題.



 字詞句段篇系列答案
字詞句段篇系列答案 截至2014年11月27目,我國機動車駕駛人數量突破3億大關,年均增長超過兩千萬.為了解我地區駕駛預考人員的現狀,選擇A,B,C三個駕校進行調查.參加各駕校科目一預考人數如下:
截至2014年11月27目,我國機動車駕駛人數量突破3億大關,年均增長超過兩千萬.為了解我地區駕駛預考人員的現狀,選擇A,B,C三個駕校進行調查.參加各駕校科目一預考人數如下: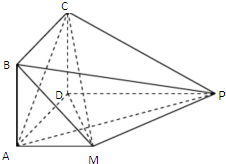 如圖,四邊形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如圖,四邊形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=