
已知拋物線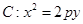 (
(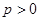 )上一點
)上一點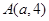 到其準線的距離為
到其準線的距離為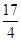 .
.
(Ⅰ)求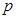 與
與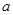 的值;
的值;
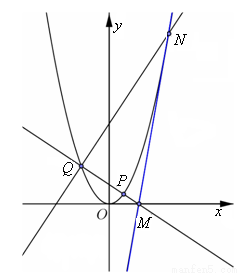
(Ⅱ)設拋物線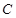 上動點
上動點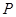 的橫坐標為
的橫坐標為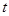 (
(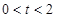 ),過點
),過點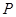 的直線交
的直線交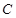 于另一點
于另一點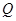 ,交
,交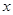 軸于
軸于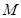 點(直線
點(直線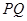 的斜率記作
的斜率記作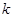 ).過點
).過點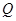 作
作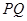 的垂線交
的垂線交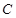 于另一點
于另一點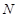 .若
.若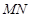 恰好是
恰好是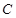 的切線,問
的切線,問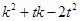 是否為定值?若是,求出該定值;若不是,說明理由.
是否為定值?若是,求出該定值;若不是,說明理由.
(Ⅰ) ,
,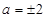 (Ⅱ)定值
(Ⅱ)定值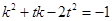
【解析】
試題分析:(Ⅰ)由拋物線方程得其準線方程: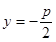 ,點
,點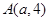 到其準線的距離即
到其準線的距離即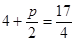 ,解得
,解得 ,
,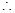 拋物線方程為:
拋物線方程為: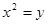 ,將
,將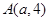 代入拋物線方程,解得
代入拋物線方程,解得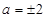 .
.
(Ⅱ)由題意知,過點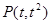 的直線
的直線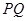 斜率
斜率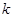 不為
不為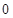 ,
,
則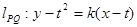 ,當
,當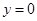 時,
時, 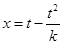 ,則
,則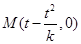 .
.
聯立方程 ,消去
,消去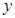 ,得
,得 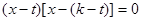 ,
,
解得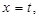 或
或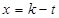 ,
,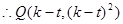 ,
,
而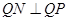 ,
,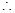 直線
直線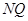 斜率為
斜率為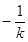 ,
,
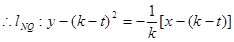 ,聯立方程
,聯立方程
消去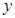 ,得
,得 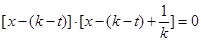 ,
,
解得: ,或
,或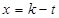 ,
,
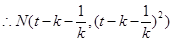 ,
,
所以,拋物線在點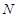 處切線斜率:
處切線斜率: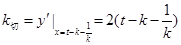 ,
,
于是拋物線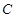 在點
在點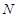 處切線的方程是:
處切線的方程是:
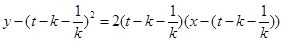 ,①
,①
將點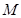 的坐標代入①,得
的坐標代入①,得
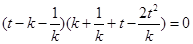 ,
,
因為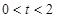 ,所以
,所以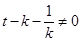 ,故
,故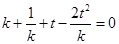 ,
,
整理得 ,
,
即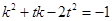 為定值.
為定值.
考點:拋物線定義方程及直線與拋物線的位置關系
點評:第一問的求解采用拋物線定義:拋物線上的點到焦點的距離等于到準線的距離,較簡單,第二問直線與拋物線相交為背景,常聯立方程組轉化,本題第二問計算量較大,學生在數據處理時可能出問題


科目:高中數學 來源: 題型:
已知拋物線![]() :
:![]() 上一點
上一點![]() 到其焦點的距離為
到其焦點的距離為![]() .
.
(I)求![]() 與
與![]() 的值;
的值;
(II)設拋物線![]() 上一點
上一點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 的直線交
的直線交![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于另一點
于另一點![]() .若
.若![]() 是
是![]() 的切線,求
的切線,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
|
(I)求![]() 與
與![]() 的值;
的值;
(II)設拋物線![]() 上一點
上一點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 的直線交
的直線交![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于另一點
于另一點![]() .若
.若![]() 是
是![]() 的切線,求
的切線,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
|
(I)求![]() 與
與![]() 的值;
的值;
(II)設拋物線![]() 上一點
上一點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 的直線交
的直線交![]() 于另一點
于另一點![]() ,交
,交![]() 軸于
軸于
點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于另一點
于另一點![]() .若
.若![]() 是
是![]() 的切線,求
的切線,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2011年浙江省杭州市高二寒假作業數學卷選修1-1 題型:解答題
已知拋物線 :
: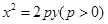 上一點
上一點 到其焦點的距離為
到其焦點的距離為 .
.
(I)求 與
與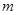 的值;
的值;
(II)設拋物線 上一點
上一點 的橫坐標為
的橫坐標為 ,過
,過 的直線交
的直線交 于另一點
于另一點 ,交
,交 軸于點
軸于點 ,過點
,過點 作
作 的垂線交
的垂線交 于另一點
于另一點 .若
.若 是
是 的切線,求
的切線,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2009年普通高等學校招生全國統一考試文科數學(浙江卷) 題型:解答題
已知拋物線 :
: 上一點
上一點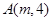 到其焦點的距離為
到其焦點的距離為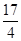 .
.
(I)求 與
與 的值;
的值;
(II)設拋物線 上一點
上一點 的橫坐標為
的橫坐標為 ,過
,過 的直線交
的直線交 于另一點
于另一點 ,交
,交 軸于點
軸于點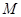 ,過點
,過點 作
作 的垂線交
的垂線交 于另一點
于另一點 .若
.若 是
是 的切線,求
的切線,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com