
已知:函數![]() .
.
(I)證明:f(x)與f-1(x)的交點必在在直線y=x上.
(II)是否存在一對反函數圖象的交點不一定在直線y=x上,若存在,請舉例說明;若不存,請說明理由.
(III)研究(I)和(II),能否得出一般性的結論,并進行證明.
|
解答:(I)y=2x+1與其反函數 (II) (III)研究(I)和(II)能得出:如果函數f(x)是增函數,并且f(x)的圖象與其反函數的圖象有交點,則交點一定在直線y=x上; 如果函數f(x)是減函數,并且f(x)的圖象與其反函數的圖象有交點,則交點不一定在直線y=x上. 證明:設點(a,b)是f(x)的圖象與其反函數圖象的任一交點,由于原函數與反函數圖象關于直線y=x對稱,則點(b,a)也是f(x)的圖象與其反函數圖象的交點,且有b=f(a),a=f(b) 若a=b時,交點顯然在直線y=x上. 若a<b,且f(x)是增函數時,有f(b)<f(a),從而有b<a,矛盾;若b<a且f(x)是增函數時,有f(a)<f(b),從而有a<b,矛盾. 若a<b,且f(x)是減函數,有f(b)<f(a),從而a<b成立,此時交點不在直線y=x上;同理,b<a且f(x)是減函數時,交點也不在直線y=x上. 綜上所述,如果函數f(x)是增函數,并且f(x)的圖象與其反函數的圖象有交點,則交點一定在直線y=x上; 如果函數f(x)是減函數,并且f(x)的圖象與其反函數的圖象有交點,則交點不一定在直線y=x上. |
|
分析:問題(I)易于解答,而問題(II)解答必須認真思考f(x)的性質,從性質的差異去尋求特例.問題(III)的證明著眼于函數單調性的差異解答. 說明:試題緊扣江蘇新考綱,突顯解決問題的探索性和研究性.試題難度較大. |


 計算高手系列答案
計算高手系列答案科目:高中數學 來源:2013年甘肅省定西市文峰中學高三新課標數學模擬試卷(一)(解析版) 題型:解答題
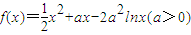
查看答案和解析>>
科目:高中數學 來源:2011年山東省濟寧一中高三一輪復習質量驗收數學試卷(文科)(解析版) 題型:解答題
 ,函數
,函數
查看答案和解析>>
科目:高中數學 來源:2011年陜西省咸陽市高考模擬考試數學試卷((理科)(解析版) 題型:解答題
 ,函數
,函數
查看答案和解析>>
科目:高中數學 來源:2011年陜西省咸陽市高考數學模擬試卷(文科)(解析版) 題型:解答題
 ,函數
,函數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com