已知8cos(2α+β)+5cosβ=0,求tan(α+β)•tanα的值.
【答案】
分析:通過變形使2α+β=(α+β)+α,β=(α+β)-α,進而利用兩角和公式化簡求得tan(α+β)•tanα
解答:解:∵2α+β=(α+β)+α,β=(α+β)-α,
∴8cos[(α+β)+α]+5cos[(α+β)-a]=0,
得13cos(α+β)cosα=3sin(α+β)sinα,
若cos(α+β)cosα≠0,則
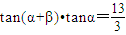
,
若cos(α+β)cosα=0,tan(α+β)•tanα無意義.
點評:本題主要考查三角函數中的兩角和公式的運用.角的和、差、倍、半具有相對性,如β=(α+β)-α=(β-α)+α,2α=(α+β)+(α-β),2α+β=(α+β)+α等,解題過程中應充分利用這種變形.

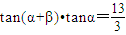 ,
,

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案