【題目】已知函數
，其中
.
（1）討論
的單調性；
（2）當
時，證明:
；
（3）試比較
與
，并證明你的結論。
【答案】（1）見解析；（2）見解析；（3）見解析
【解析】
（1）求得
，對
的范圍分類討論即可求得
的單調性。
（2）將
轉化成
，證明
恒成立，利用導數求得
，問題得證。
（3）由（2）可得：
，整理得：
，所以
，整理
得：
利用
即可得：
，問題得解。
（1）函數的定義域為：
，
①當
時，
，所以在上單調遞增
②當
時，令
，解得
．
當
時，
，所以
， 所以在
上單調遞減；
當
時，
，所以，所以在
上單調遞增．
綜上，當時，函數在上單調遞增；
當時，函數在上單調遞減，在上單調遞增.
（2）當 
時，
，要證明，
即證，即證：.
設
，則
，令
得，
.
當
時，
，當
時，
.
所以為極大值點，且
在處取得最大值。
所以，即。故.
（3）證明：（當且僅當時等號成立），即,
則有
+
,
故：+
科目：高中數學 來源： 題型：
【題目】如圖，正方體
的棱長為1，線段
上有兩個動點
，且
，現有如下四個結論：
；
平面
；
三棱錐
的體積為定值；
異面直線
所成的角為定值，
其中正確結論的序號是______．
查看答案和解析>>
科目：高中數學 來源： 題型：
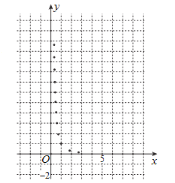
【題目】某學生為了測試煤氣灶燒水如何節(jié)省煤氣的問題設計了一個實驗，并獲得了煤氣開關旋鈕旋轉的弧度數
與燒開一壺水所用時間
的一組數據，且作了一定的數據處理(如下表)，得到了散點圖(如下圖)．
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中
．
（1）根據散點圖判斷，
與
哪一個更適宜作燒水時間關于開關旋鈕旋轉的弧度數的回歸方程類型?(不必說明理由)
（2）根據判斷結果和表中數據，建立關的回歸方程；
（3）若旋轉的弧度數與單位時間內煤氣輸出量
成正比，那么為多少時，燒開一壺水最省煤氣？
附：對于一組數據
，其回歸直線
的斜率和截距的最小二乘估計分別為
．
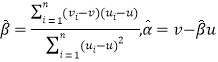查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業(yè)甲,乙兩個研發(fā)小組,他們研發(fā)新產品成功的概率分別為
和
,現安排甲組研發(fā)新產品
,乙組研發(fā)新產品
.設甲,乙兩組的研發(fā)是相互獨立的.
(1)求至少有一種新產品研發(fā)成功的概率;
(2)若新產品
研發(fā)成功,預計企業(yè)可獲得
萬元,若新產品
研發(fā)成功,預計企業(yè)可獲得利潤
萬元,求該企業(yè)可獲得利潤的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數
在一個周期內的圖象如圖所示，A為圖象的最高點，B，C為
的圖象與x軸的交點，且
為等邊三角形.將函數的圖象上各點的橫坐標變?yōu)樵瓉淼?/span>
倍后，再向右平移
個單位，得到函數
的圖象.
（1）求函數
的解析式；
（2）若不等式
對任意
恒成立，求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1＝1， 
，其中n∈N*．
（1）設
，求證：數列{bn}是等差數列，并求出{an}的通項公式．
（2）設
，數列{cncn+2}的前n項和為Tn，是否存在正整數m，使得
對于n∈N*，恒成立？若存在，求出m的最小值；若不存在，請說明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
