Question

已知數列{a_n}的前n項和為S_n，a₁=1，且3a_n+1+2S_n=3（π為正整數）．
（1）求數列{a_n}的通項公式；
（2）記S=a₁+a₂+…+a_n+…若對任意正整數n，kS≤S_n恒成立，求實數k的最大值．

Answer 1

【答案】分析：（1）3a_n+1+2s_n=3，3a_n+2s_n-1=3，兩式相減，得3a_n+1-3a_n+2（S_n-S_n-1）=0，由此能求出數列{a_n}的通項公式．
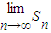
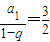
（2）S==，由此能求出k的最大值．
解答：解：（1）由題設條件得
3a_n+1+2s_n=3，3a_n+2s_n-1=3
兩式相減，得3a_n+1-3a_n+2（S_n-S_n-1）=0，
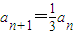
即，n＞1 又，
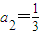
所以通項為：．
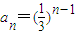
（2）S==，
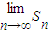
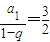
要kS≤Sn恒成立，由于Sn遞增
所以只要kS=S₁，即k的最大值為．
點評：本題考查數列的遞推式和數列性質的綜合應用，解題時要認真審題，仔細解答，注意不等式和數列的綜合應用．