
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
: ![]() 的左焦點是
的左焦點是![]() ,離心率為
,離心率為![]() ,且
,且![]() 上任意一點
上任意一點![]() 到
到![]() 的最短距離為
的最短距離為![]() .
.
(1)求![]() 的方程;
的方程;
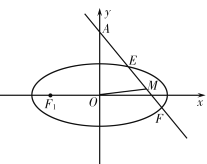
(2)過點![]() 的直線
的直線![]() (不過原點)與
(不過原點)與![]() 交于兩點
交于兩點![]() 、
、![]() ,
, ![]() 為線段
為線段![]() 的中點.
的中點.
(i)證明:直線![]() 與
與![]() 的斜率乘積為定值;
的斜率乘積為定值;
(ii)求![]() 面積的最大值及此時
面積的最大值及此時![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)(i)見解析;(ii)
;(2)(i)見解析;(ii)![]() 面積的最大值是
面積的最大值是![]() ,此時
,此時![]() 的斜率為
的斜率為![]() .
.
【解析】試題分析:(1)由題設可以得到關于![]() 的方程組為
的方程組為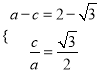 ,從而
,從而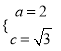 ,故
,故![]() ,所以橢圓
,所以橢圓![]() 的方程為
的方程為![]() .(2)設直線
.(2)設直線![]() 為:
為: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,聯立直線的方程和橢圓的方程并消元后可以得到
,聯立直線的方程和橢圓的方程并消元后可以得到![]() ,利用韋達定理得到
,利用韋達定理得到![]() ,故
,故![]() ,從而
,從而![]() 為定值.利用弦長公式和點到直線的距離可得
為定值.利用弦長公式和點到直線的距離可得![]() ,令
,令![]() ,從而
,從而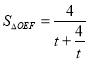 ,最后利用基本不等式可以得到面積的最大值為
,最后利用基本不等式可以得到面積的最大值為![]() 且此時
且此時![]() 也就是
也就是![]() .
.
解析:(1)由題意得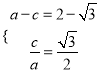 ,解得
,解得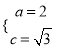 ,∴
,∴![]() ,
, ![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
(2)(i)設直線![]() 為:
為: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由題意得
,由題意得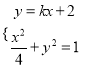 ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,由韋達定理得:
,由韋達定理得: ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴直線
,∴直線![]() 與
與![]() 的斜率乘積為定值.
的斜率乘積為定值.
(ii)由(i)可知: ![]()
![]()
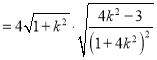
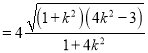 ,又點
,又點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
∴![]() 的面積
的面積![]()
![]()
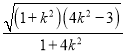
![]() ,令
,令![]() ,則
,則![]() ,∴
,∴![]()
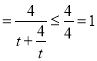 ,當且僅當
,當且僅當![]() 時等號成立,此時
時等號成立,此時![]() ,且滿足
,且滿足![]() ,∴
,∴![]() 面積的最大值是
面積的最大值是![]() ,此時
,此時![]() 的斜率為
的斜率為![]() .
.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,側面
中,側面![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
, ![]() ,四棱錐
,四棱錐![]() 的體積為2,點
的體積為2,點![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,且
,且![]() 在
在![]() 上,點
上,點![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(Ⅰ)證明:直線![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
, ![]() 為正常數),現假定生產量與銷售量相等,已知生產該產品
為正常數),現假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等邊三角形![]() 的邊長為
的邊長為![]() ,且其
,且其
三個頂點均在拋物線![]() 上.
上.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)設動直線![]() 與拋物線
與拋物線![]() 相切于點
相切于點![]() ,與直線
,與直線![]()
相交于點![]() .證明以
.證明以![]() 為直徑的圓恒過
為直徑的圓恒過![]() 軸上某定點.
軸上某定點.

查看答案和解析>>
科目:高中數學 來源: 題型:
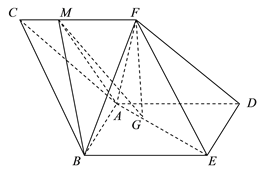
【題目】一裝有水的直三棱柱ABC-A1B1C1容器(厚度忽略不計),上下底面均為邊長為5的正三角形,側棱為10,側面AA1B1B水平放置,如圖所示,點D、E、F、G分別在棱CA、CB、C1B1、C1A1上,水面恰好過點D,E,F,C,且CD=2

(1)證明:DE∥AB;
(Ⅱ)若底面ABC水平放置時,求水面的高
查看答案和解析>>
科目:高中數學 來源: 題型:
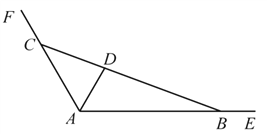
【題目】如圖,某大型景區有兩條直線型觀光路線![]() ,
, ![]() ,
,![]() ,點
,點![]() 位于
位于![]() 的平分線上,且與頂點
的平分線上,且與頂點![]() 相距1公里.現準備過點
相距1公里.現準備過點![]() 安裝一直線型隔離網
安裝一直線型隔離網![]() (
(![]() 分別在
分別在![]() 和
和![]() 上),圍出三角形區域
上),圍出三角形區域![]() ,且
,且![]() 和
和![]() 都不超過5公里.設
都不超過5公里.設![]() ,
, ![]() (單位:公里).
(單位:公里).
(Ⅰ)求![]() 的關系式;
的關系式;
(Ⅱ)景區需要對兩個三角形區域![]() ,
, ![]() 進行綠化.經測算,
進行綠化.經測算, ![]() 區城每平方公里的綠化費用是
區城每平方公里的綠化費用是![]() 區域的兩倍,試確定
區域的兩倍,試確定![]() 的值,使得所需的總費用最少.
的值,使得所需的總費用最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
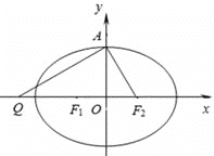
【題目】設橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為A,過點A與
,上頂點為A,過點A與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() ,若過
,若過![]() ,
, ![]() ,
, ![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切.過定點
相切.過定點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(點
兩點(點![]() 在點
在點![]() ,
, ![]() 之間).
之間).
(Ⅰ)求橢圓![]() 的方程;(Ⅱ)若實數
的方程;(Ⅱ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
在平面直角坐標系xOy 中,曲線C的參數方程為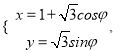 (
(![]() 是參數,0≤
是參數,0≤![]() ≤π),以O 為極點,以x 軸的正半軸為極軸,建立極坐標系.
≤π),以O 為極點,以x 軸的正半軸為極軸,建立極坐標系.
(Ⅰ)求曲線C 的極坐標方程;
(Ⅱ)直線l1,的極坐標方程是2psin(θ+![]() )+
)+![]() =0,直線l2:θ =
=0,直線l2:θ =![]() 與曲線C的交點為P,與直線l1的交點為Q,求線段PQ的長.
與曲線C的交點為P,與直線l1的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司租賃甲、乙兩種設備生產A,B兩類產品,甲種設備每天能生產A類產品5件和B類產品10件,乙種設備每天能生產A類產品6件和B類產品20件。已知設備甲每天的租賃費為200元,設備乙每天的租賃費為300元,現該公司至少要生產A類產品50件,B類產品140件,所需租賃費最少為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com