
【題目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三個向量,其中
是同一平面上的三個向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐標.
的坐標.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 與2
與2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 與
與 ![]() 的夾角θ
的夾角θ
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中, 曲線
中, 曲線![]() 的參數方程為
的參數方程為![]() 為參數) ;在以原點
為參數) ;在以原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中, 曲線
軸的正半軸為極軸的極坐標系中, 曲線![]() 的極坐標參數方程為
的極坐標參數方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() 與曲線
與曲線![]() ,
,![]() 的交點分別為
的交點分別為![]() (
(![]() 異于原點). 當斜率
異于原點). 當斜率![]() 時, 求
時, 求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C方程為 ![]() (a>b>0),左、右焦點分別是F1 , F2 , 若橢圓C上的點P(1,
(a>b>0),左、右焦點分別是F1 , F2 , 若橢圓C上的點P(1, ![]() )到F1 , F2的距離和等于4. (Ⅰ)寫出橢圓C的方程和焦點坐標;
)到F1 , F2的距離和等于4. (Ⅰ)寫出橢圓C的方程和焦點坐標;
(Ⅱ)設點Q是橢圓C的動點,求線段F1Q中點T的軌跡方程;
(Ⅲ)直線l過定點M(0,2),且與橢圓C交于不同的兩點A,B,若∠AOB為銳角(O為坐標原點),求直線l的斜率k0的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圓,求m的取值范圍;
(2)若(1)中的圓與直線x+2y﹣4=0相交于M、N兩點,且OM⊥ON(O為坐標原點),求m;
(3)在(2)的條件下,求以MN為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在![]() 中,
中, ![]() 的中點為
的中點為![]() ,且
,且![]() ,點
,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .固定邊
.固定邊![]() ,在平面內移動頂點
,在平面內移動頂點![]() ,使得圓
,使得圓![]() 與邊
與邊![]() ,邊
,邊![]() 的延長線相切,并始終與
的延長線相切,并始終與![]() 的延長線相切于點
的延長線相切于點![]() ,記頂點
,記頂點![]() 的軌跡為曲線
的軌跡為曲線![]() .以
.以![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 為坐標原點如圖所示建立平面直角坐標系.
為坐標原點如圖所示建立平面直角坐標系.
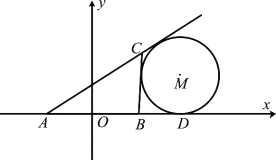
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設動直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,且以
兩點,且以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在(﹣∞,0)∪(0,+∞)上的函數f(x),如果對于任意給定的等比數列{an},{f(an)}仍是等比數列,則稱f(x)為“保等比數列函數”.現有定義在(﹣∞,0)∪(0,+∞)上的如下函數:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.則其中是“保等比數列函數”的f(x)的序號為( )
;④f(x)=ln|x|.則其中是“保等比數列函數”的f(x)的序號為( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() ,半徑為
,半徑為![]() 的圓
的圓![]() 與
與![]() 相切,圓心
相切,圓心![]() 在
在![]() 軸上且在直線
軸上且在直線![]() 的上方.
的上方.
(Ⅰ)求圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線與圓
的直線與圓![]() 交于
交于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),問在
軸上方),問在![]() 軸正半軸上是否存在點
軸正半軸上是否存在點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列函數中,在其定義域內既是奇函數又是減函數的是( )
·(1)y=﹣|x|(x∈R)(2)y=﹣x3﹣x(x∈R)(3)y=( ![]() )x(x∈R)(4)y=﹣x+
)x(x∈R)(4)y=﹣x+ ![]() .
.
A.(2)
B.(1)(3)
C.(4)
D.(2)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王創建了一個由他和甲、乙、丙共4人組成的微信群,并向該群發紅包,每次發紅包的個數為1個(小王自己不搶),假設甲、乙、丙3人每次搶得紅包的概率相同.
(Ⅰ)若小王發2次紅包,求甲恰有1次搶得紅包的概率;
(Ⅱ)若小王發3次紅包,其中第1,2次,每次發5元的紅包,第3次發10元的紅包,記乙搶得所有紅包的錢數之和為X,求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com