
| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
分析 (1)設拋物線方程為y2=mx,代入4個點,可得m,檢驗可知m=1成立,再將其余兩個點代入橢圓方程,解得a,b,進而得到橢圓方程;
(2)①討論當直線AB的斜率為0時,設P(4,y0),可得結論;當直線AB的斜率不為0時,
設AB:x=ty+2,代入x2+2y2=8,消去x,運用韋達定理和直線的斜率公式,化簡整理,再結合向量的坐標表示,向量模的平方即為向量的平方,結合二次函數最值求法,可得t的值,進而得到所求直線方程.
解答 解:(1)設拋物線方程為y2=mx,分別將四個點代入解得m=-1,m=1,m=$\frac{\sqrt{6}}{6}$,m=1,
故拋物線方程為y2=x;即點(2,-$\sqrt{2}$)和(9,3)在拋物線上.
因此(-2,$\sqrt{2}$),($\sqrt{6}$,-1)兩個點為橢圓C1上兩點,
設橢圓方程為:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
將上述兩個點坐標代入$\frac{4}{{a}^{2}}$+$\frac{2}{{b}^{2}}$=1,$\frac{6}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
解得:a2=8,b2=4,
故橢圓方程為:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1. (4分)
(2)①證明:當直線AB的斜率為0時,
設P(4,y0),則kPA+kPB=y0=2kPF,直線PA,PF,PB的斜率成等差數列; (5分)
當直線AB的斜率不為0時,
設AB:x=ty+2,代入x2+2y2=8,消去x,可得(2+t2)y2+4ty-4=0,
設A(x1,y1),B(x2,y2),則y1+y2=-$\frac{4t}{2+{t}^{2}}$,y1y2=-$\frac{4}{2+{t}^{2}}$,
則有:kPA+kPB=$\frac{{y}_{0}-{y}_{1}}{2-t{y}_{1}}$+$\frac{{y}_{0}-{y}_{2}}{2-t{y}_{2}}$=$\frac{4{y}_{0}-(2+t{y}_{0})({y}_{1}+{y}_{2})+2t{y}_{1}{y}_{2}}{4-2t({y}_{1}+{y}_{2})+{t}^{2}{y}_{1}{y}_{2}}$=y0=2kPF,
則直線PA,PF,PB的斜率成等差數列 (7分)
$\overrightarrow{②}$因為$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],所以$\frac{{y}_{1}}{{y}_{2}}$=λ,且λ<0.
又y1+y2=-$\frac{4t}{2+{t}^{2}}$,y1y2=-$\frac{4}{2+{t}^{2}}$,
則$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{{{y}_{1}}^{2}+2{y}_{1}{y}_{2}+{{y}_{2}}^{2}}{{y}_{1}{y}_{2}}$=λ+$\frac{1}{λ}$+2,
又$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=-$\frac{4{t}^{2}}{2+{t}^{2}}$,
即λ+$\frac{1}{λ}$+2=-$\frac{4{t}^{2}}{2+{t}^{2}}$,
由λ∈[-2,-1],得λ+$\frac{1}{λ}$∈[-$\frac{5}{2}$,-2],即t2∈[0,$\frac{2}{7}$],
因為P(4,0),$\overrightarrow{PA}$=(x1-4,y1),$\overrightarrow{PB}$=(x2-4,y2),
所以$\overrightarrow{PA}$+$\overrightarrow{PB}$=(x1+x2-8,y1+y2)=(ty1+ty2-4,y1+y2),
故|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2=(ty1+ty2-4)2+(y1+y2)2=(-$\frac{4{t}^{2}}{2+{t}^{2}}$-4)2+(-$\frac{4t}{2+{t}^{2}}$)2=$\frac{(8{t}^{2}+8)^{2}+16{t}^{2}}{(2+{t}^{2})^{2}}$,
令m=2+t2(m∈[2,$\frac{16}{7}$]),則|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2=$\frac{(8m-8)^{2}+16(m-2)}{{m}^{2}}$=64-$\frac{112}{m}$+$\frac{32}{{m}^{2}}$
=2($\frac{4}{m}$-7)2-34=32($\frac{1}{m}$-$\frac{7}{4}$)2-34,
當$\frac{1}{m}$=$\frac{7}{16}$ 即t2=$\frac{2}{7}$時,|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2的值最大,
此時方程為x=±$\frac{\sqrt{14}}{7}$y+2. (13分)
點評 本題考查橢圓和拋物線方程的求法,注意運用代入法,考查直線和橢圓方程聯立,運用韋達定理,以及向量坐標表示,考查化簡整理的運算能力,屬于難題.


科目:高中數學 來源:2016-2017學年河北正定中學高二上月考一數學(理)試卷(解析版) 題型:選擇題
已知直線 :
: 與直線
與直線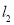 :
: 平行,且
平行,且 與圓
與圓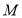 :
: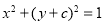 相切,則
相切,則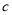 的值為( )
的值為( )
A. B.
B. C.
C.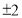 D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知拋物線C:y2=2px(p>0)的準線為l,焦點為F,圓M的圓心在x軸的正半軸上,且與y軸相切,過原點作傾斜角為$\frac{π}{3}$的直線t,交l于點A,交圓M于點B,且|AO|=|OB|=2.
如圖,已知拋物線C:y2=2px(p>0)的準線為l,焦點為F,圓M的圓心在x軸的正半軸上,且與y軸相切,過原點作傾斜角為$\frac{π}{3}$的直線t,交l于點A,交圓M于點B,且|AO|=|OB|=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com