
【題目】下列五個命題:①直線![]() 的斜率
的斜率![]() ,則直線
,則直線![]() 的傾斜角的范圍是
的傾斜角的范圍是![]() ;②直線
;②直線![]() :
:![]() 與過
與過![]() ,
,![]() 兩點的線段相交,則
兩點的線段相交,則![]() 或
或![]() ;③如果實數
;③如果實數![]() ,
,![]() 滿足方程
滿足方程![]() ,那么
,那么![]() 的最大值為
的最大值為![]() ;④直線
;④直線![]() 與橢圓
與橢圓![]() 恒有公共點,則
恒有公共點,則![]() 的取值范圍是
的取值范圍是![]() ;⑤方程
;⑤方程![]() 表示圓的充要條件是
表示圓的充要條件是![]() 或
或![]() ;正確的是( )
;正確的是( )
A.②③B.③④C.②⑤D.②③⑤
【答案】D
【解析】
①根據正切函數在![]() 圖像,可判斷直線
圖像,可判斷直線![]() 的傾斜角的范圍是
的傾斜角的范圍是![]() ,所以選項
,所以選項![]() 不正確;
不正確;
②直線![]() :
:![]() 過
過![]() ,結合圖像可得,直線
,結合圖像可得,直線![]() :
:![]() 與過
與過![]() ,
,![]() 兩點的線段相交時,
兩點的線段相交時,![]() 或
或![]() ,正確;
,正確;
③ 設![]() ,則
,則![]() ,轉化為圓上的點與坐標原點連線的斜率,
,轉化為圓上的點與坐標原點連線的斜率,![]() 的最大值時,直線與圓相切,求出
的最大值時,直線與圓相切,求出![]() 的最大值為
的最大值為![]() ,正確;
,正確;
④直線方程![]() 過
過![]() 點,直線與橢圓恒有公共點,只需點
點,直線與橢圓恒有公共點,只需點![]() 點在橢圓內或橢圓上,得到
點在橢圓內或橢圓上,得到![]() ,結合方程
,結合方程![]() 表示橢圓,
表示橢圓,![]() ,因此不正確;
,因此不正確;
⑤方程![]() 配方,得出方程表示圓滿足的條件,
配方,得出方程表示圓滿足的條件,![]() ,解得
,解得![]() 或
或![]() ,因此正確.
,因此正確.
①設直線![]() 的傾斜角為
的傾斜角為![]() ,直線
,直線![]() 的斜率
的斜率![]() ,則
,則![]() ,
,
直線![]() 的傾斜角的范圍是
的傾斜角的范圍是![]() ,因此不正確;
,因此不正確;
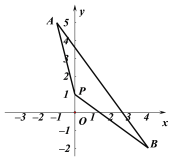
②直線![]() :
:![]() 與過
與過![]() ,
,![]() 兩點的線段相交,
兩點的線段相交,
直線![]() 經過
經過![]() ,
,![]() ,
,![]() ,
,
則![]() 或
或![]() ,正確;
,正確;
③如果實數![]() ,
,![]() 滿足方程
滿足方程![]() ,設
,設![]() ,則
,則![]() ,
,
當此直線與圓相切時,![]() ,解得
,解得![]() ,
,
因此![]() 的最大值為
的最大值為![]() ,正確;
,正確;
④直線方程![]() 過
過![]() 點,直線與橢圓恒有公共點,
點,直線與橢圓恒有公共點,
點![]() 點在橢圓內或橢圓上,
點在橢圓內或橢圓上,![]()
![]() ,且
,且![]() ,因此不正確;
,因此不正確;
⑤方程![]() 配方為:
配方為:
![]() ,
,
表示圓的充要條件是![]() ,
,
解得![]() 或
或![]() ,因此正確.
,因此正確.
綜上可得:正確的是②③⑤.
故選:D.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某工廠對一批產品進行了抽樣檢測.右圖是根據抽樣檢測后的產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),[100,102),[102,104),[104,106],已知樣本中產品凈重小于100克的個數是36,則樣本中凈重大于或等于98克并且小于104克的產品的個數是( ).
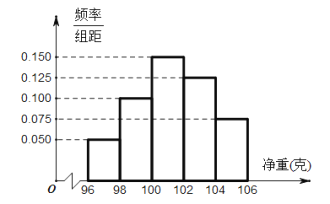
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若<<0,則下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正確的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健身機構統計了去年該機構所有消費者的消費金額(單位:元),如圖所示:
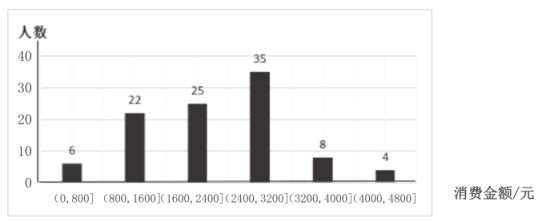
(1)現從去年的消費金額超過3200元的消費者中隨機抽取2人,求至少有1位消費者,其去年的消費者金額在![]() 的范圍內的概率;
的范圍內的概率;
(2)針對這些消費者,該健身機構今年欲實施入會制,詳情如下表:
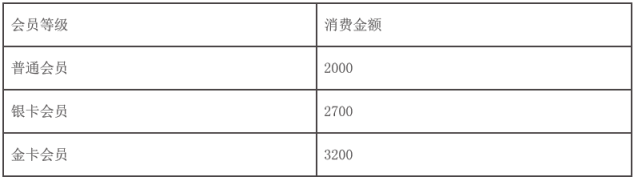
預計去年消費金額在![]() 內的消費者今年都將會申請辦理普通會員,消費金額在
內的消費者今年都將會申請辦理普通會員,消費金額在![]() 內的消費者都將會申請辦理銀卡會員,消費金額在
內的消費者都將會申請辦理銀卡會員,消費金額在![]() 內的消費者都將會申請辦理金卡會員,消費者在申請辦理會員時,需一次性繳清相應等級的消費金額,該健身機構在今年底將針對這些消費者舉辦消費返利活動,現有如下兩種預設方案:
內的消費者都將會申請辦理金卡會員,消費者在申請辦理會員時,需一次性繳清相應等級的消費金額,該健身機構在今年底將針對這些消費者舉辦消費返利活動,現有如下兩種預設方案:
方案1:按分層抽樣從普通會員,銀卡會員,金卡會員中總共抽取25位“幸運之星”給予獎勵:
普通會員中的“幸運之星”每人獎勵500元;銀卡會員中的“幸運之星”每人獎勵600元;金卡會員中的“幸運之星”每人獎勵800元.
方案二:每位會員均可參加摸獎游戲,游戲規則如下:從一個裝有3個白球、2個紅球(球只有顏色不同)的箱子中,有放回地摸三次球,每次只能摸一個球,若摸到紅球的總數為2,則可獲得200元獎勵金;若摸到紅球的總數為3,則可獲得300元獎勵金;其他情況不給予獎勵. 規定每位普通會員均可參加1次摸獎游戲;每位銀卡會員均可參加2次摸獎游戲;每位金卡會員均可參加3次摸獎游戲(每次摸獎的結果相互獨立)
請你預測哪一種返利活動方案該健身機構的投資較少?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓上存在一點
,且橢圓上存在一點![]() ,滿足
,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】棱長為1的正方體![]() 中,點
中,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上運動(不包括線段端點),且
上運動(不包括線段端點),且![]() .以下結論:①
.以下結論:①![]() ;②若點
;②若點![]() 、
、![]() 分別為線段
分別為線段![]() 、
、![]() 的中點,則由線
的中點,則由線![]() 與
與![]() 確定的平面在正方體
確定的平面在正方體![]() 上的截面為等邊三角形;③四面體
上的截面為等邊三角形;③四面體![]() 的體積的最大值為
的體積的最大值為![]() ;④直線
;④直線![]() 與直線
與直線![]() 的夾角為定值.其中正確的結論為______.(填序號)
的夾角為定值.其中正確的結論為______.(填序號)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:函數![]() ,數列
,數列![]() 對
對![]() ,總有
,總有 ;
;
(1)求![]() 的通項公式;
的通項公式;
(2)設![]() 是數列
是數列![]() 的前
的前![]() 項和,且
項和,且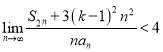 ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 滿足:①
滿足:①![]() 為
為![]() 的子數列(即
的子數列(即![]() 中每一項都是
中每一項都是![]() 的項,且按在
的項,且按在![]() 中的順序排列);②
中的順序排列);②![]() 為無窮等比數列,它的各項和為
為無窮等比數列,它的各項和為![]() ,這樣的數列是否存在?若存在,求出所有符合條件的數列
,這樣的數列是否存在?若存在,求出所有符合條件的數列![]() .寫出它的通項公式,并證明你的結論;若不存在,說明理由.
.寫出它的通項公式,并證明你的結論;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com