
【題目】為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)= ![]() (0≤x≤10),若不建隔熱層,每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(0≤x≤10),若不建隔熱層,每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(Ⅰ)求k的值及f(x)的表達式.
(Ⅱ)隔熱層修建多厚時,總費用f(x)達到最小,并求最小值.
【答案】解:(Ⅰ)設隔熱層厚度為xcm,由題設,每年能源消耗費用為 ![]() .
.
再由C(0)=8,得k=40,因此 ![]() .
.
而建造費用為C1(x)=6x,最后得隔熱層建造費用與20年的能源消耗費用之和![]()
(Ⅱ) ![]() ,令f'(x)=0,即
,令f'(x)=0,即 ![]() .
.
解得x=5, ![]() (舍去).當0<x<5時,f′(x)<0,當5<x<10時,f′(x)>0,故x=5是f(x)的最小值點,對應的最小值為
(舍去).當0<x<5時,f′(x)<0,當5<x<10時,f′(x)>0,故x=5是f(x)的最小值點,對應的最小值為![]() .
.
當隔熱層修建5cm厚時,總費用達到最小值為70萬元.
【解析】(Ⅰ)由題意可得每年能源消耗費用為 C ( x ) = ![]() ,又根據C(0)=8,得k=40,因此 C ( x ) =
,又根據C(0)=8,得k=40,因此 C ( x ) =![]() ,建造費用為C1(x)=6x,最后得隔熱層建造費用與20年的能源消耗費用之和 f ( x ) = 20 C ( x ) + C1 ( x ) = 20 ×
,建造費用為C1(x)=6x,最后得隔熱層建造費用與20年的能源消耗費用之和 f ( x ) = 20 C ( x ) + C1 ( x ) = 20 × ![]() + 6 x =
+ 6 x = ![]() + 6 x ( 0 ≤ x ≤ 10)
+ 6 x ( 0 ≤ x ≤ 10)
(Ⅱ)根據求導求最值令f'(x)=0即![]() 解得x=5, x =
解得x=5, x = ![]() (舍去).當0<x<5時,f′(x)<0,當5<x<10時,f′(x)>0,故x=5是f(x)的最小值點,對應的最小值為 f ( 5 ) = 6 × 5 +
(舍去).當0<x<5時,f′(x)<0,當5<x<10時,f′(x)>0,故x=5是f(x)的最小值點,對應的最小值為 f ( 5 ) = 6 × 5 + ![]() = 70 .當隔熱層修建5cm厚時,總費用達到最小值為70萬元
= 70 .當隔熱層修建5cm厚時,總費用達到最小值為70萬元


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】已知點A(0,﹣2),橢圓E: ![]() +
+ ![]() =1(a>0,b>0)的離心率為
=1(a>0,b>0)的離心率為 ![]() ,F是橢圓E的右焦點,直線AF的斜率為
,F是橢圓E的右焦點,直線AF的斜率為 ![]() ,O是坐標原點.
,O是坐標原點.
(1)求E的方程;
(2)設過點A的直線l與E相交于P,Q兩點,當△OPQ的面積最大時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設數列{an+bn}是首項為1,公比為c的等比數列,求{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中錯誤的個數為:( )
①y= ![]() 的圖象關于(0,0)對稱;
的圖象關于(0,0)對稱;
②y=x3+x+1的圖象關于(0,1)對稱;
③y= ![]() 的圖象關于直線x=0對稱;
的圖象關于直線x=0對稱;
④y=sinx+cosx的圖象關于直線x= ![]() 對稱.
對稱.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】歐巴老師布置給時鎮同學這樣一份數學作業:在同一個直角坐標系中畫出四個對數函數的圖象,使它們的底數分別為 ![]() 和
和 ![]() .時鎮同學為了和暮煙同學出去玩,問大英同學借了作業本很快就抄好了,詳見如圖.第二天,歐巴老師當堂質問時鎮同學:“你畫的四條曲線中,哪條是底數為e的對數函數圖象?”時鎮同學無言以對,憋得滿臉通紅,眼看時鎮同學就要被歐巴老師訓斥一番,聰明睿智的你能不能幫他一把,回答這個問題呢?曲線才是底數為e的對數函數的圖象.
.時鎮同學為了和暮煙同學出去玩,問大英同學借了作業本很快就抄好了,詳見如圖.第二天,歐巴老師當堂質問時鎮同學:“你畫的四條曲線中,哪條是底數為e的對數函數圖象?”時鎮同學無言以對,憋得滿臉通紅,眼看時鎮同學就要被歐巴老師訓斥一番,聰明睿智的你能不能幫他一把,回答這個問題呢?曲線才是底數為e的對數函數的圖象.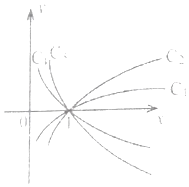
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)是定義在R上的偶函數,對任意x∈R,都有f(x)=f(x+4),且當x∈[﹣2,0]時,f(x)=( ![]() )x﹣1,若在區間(﹣2,6]內關于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三個不同的實數根,則a的取值范圍是( )
)x﹣1,若在區間(﹣2,6]內關于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三個不同的實數根,則a的取值范圍是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知α∈(0, ![]() ),β∈(0,
),β∈(0, ![]() ),且滿足
),且滿足 ![]() cos2
cos2 ![]() +
+ ![]() sin2
sin2 ![]() =
= ![]() +
+ ![]() ,sin(2017π﹣α)=
,sin(2017π﹣α)= ![]() cos(
cos( ![]() π﹣β),則α+β= .
π﹣β),則α+β= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com