【題目】有
、
、
、
四位貴賓，應分別對應坐在
、
、
、
四個席位上，現在這四人均未留意，在四個席位上隨便就座.
（1）求這四人恰好都坐在自己席位上的概率；
（2）求這四人恰好都沒坐在自己席位上的概率；
（3）求這四人恰好有
位坐在自己席位上的概率.
【答案】（1）
；（2）
；（3）
.
【解析】
以
分別表示
、
、
、
四位貴賓分別對應坐在
、
、
、
四個席位上，列舉出所有的基本事件.
（1）列舉出事件“這四人恰好都坐在自己席位上”所包含的基本事件，并利用古典概型的概率公式計算出該事件的概率；
（2）列舉出事件“這四人恰好都沒坐在自己席位上” 所包含的基本事件，并利用古典概型的概率公式計算出該事件的概率；
（3）列舉出事件“這四人恰好有
位坐在自己席位上”所包含的基本事件，并利用古典概型的概率公式計算出該事件的概率.
以分別表示、、、四位貴賓分別對應坐在、、、四個席位上，所有的基本事件有：、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
，共
個基本事件.
（1）事件“這四人恰好都坐在自己席位上”所包含的基本事件為：，因此所求概率為；
（2）事件“這四人恰好都沒坐在自己席位上”所包含的基本事件有：、、、、、、、、，共
個基本事件，因此，所求概率為
；
（3）事件“這四人恰好有位坐在自己席位上”所包含的基本事件有：、、、、、、、，共
個基本事件，因此，所求概率為
.
科目：高中數學 來源： 題型：
【題目】已知a＞0，b＞0，函數f（x）＝｜x＋a｜＋｜2x－b｜的最小值為1．
（1）證明：2a＋b＝2；
（2）若a＋2b≥tab恒成立，求實數t的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面是追蹤調查200個某種電子元件壽命（單位:
)頻率分布直方圖，如圖：
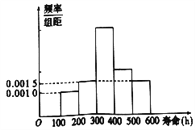
其中300-400、400-500兩組數據丟失，下面四個說法中有且只有一個與原數據相符，這個說法是( )
①壽命在300-400的頻數是90；
②壽命在400-500的矩形的面積是0.2；
③用頻率分布直方圖估計電子元件的平均壽命為：
④壽命超過
的頻率為0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列隨機事件：
①某射手射擊一次，可能命中
環，
環，
環，
，
環；
②一個小組有男生
人，女生
人，從中任選人進行活動匯報；
③一只使用中的燈泡壽命長短；
④拋出一枚質地均勻的硬幣，觀察其出現正面或反面的情況；
⑤中秋節前夕，某市有關部門調查轄區內某品牌的月餅質量，給該品牌月餅評“優”或“差”.
這些事件中，屬于古典概型的是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若方程
所表示的曲線為C，給出下列四個命題：
①若C為橢圓，則
；
②若C為雙曲線，則
或
；
③曲線C不可能是圓；
④若
，曲線C為橢圓，且焦點坐標為
；
⑤若，曲線C為雙曲線，且虛半軸長為
．
其中真命題的序號為____________.（把所有正確命題的序號都填在橫線上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在古代，直角三角形中較短的直角邊稱為“勾”,較長的直角邊稱為“股”，斜邊稱為“弦”.三國時期吳國數學家趙爽用“弦圖”( 如圖) 證明了勾股定理，證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實.”這里的“實”可以理解為面積.這個證明過程體現的是這樣一個等量關系:“兩條直角邊的乘積是兩個全等直角三角形的面積的和(朱實二 )，4個全等的直角三角形的面積的和(朱實四) 加上中間小正方形的面積(黃實) 等于大正方形的面積(弦實)”. 若弦圖中“弦實”為16，“朱實一”為
,現隨機向弦圖內投入一粒黃豆(大小忽略不計)，則其落入小正方形內的概率為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C：x2－y2＝1及直線l：y＝kx－1.
(1)若l與C有兩個不同的交點，求實數k的取值范圍；
(2)若l與C交于A，B兩點，O為坐標原點，且△AOB的面積為
，求實數k的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司有員工1000名，平均每人每年創造利潤10萬元．為了增加企業競爭力，決定優化產業結構，調整出
名員工從事第三產業，調整后他們平均每人每年創造利潤為
萬元（
），剩下的員工平均每人每年創造的利潤可以提高
．
（1）若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤，則調整員工從事第三產業的人數應在什么范圍？
（2）在（1）的條件下，若調整出的員工創造的年總利潤始終不高于剩余員工創造的年總利潤，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】計劃在某水庫建一座至多安裝3臺發電機的水電站，過去50年的水文資料顯示，水庫年入流量
(年入流量：一年內上游來水與庫區降水之和.單位：億立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超過120的年份有35年，超過120的年份有5年.將年入流量在以上三段的頻率作為相應段的概率，并假設各年的年入流量相互獨立.
（1）求未來4年中，至多1年的年入流量超過120的概率；
（2）水電站希望安裝的發電機盡可能運行，但每年發電機最多可運行臺數受年入流量
限制，并有如下關系:
年入流量 |
|
|
|
發電量最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行，則該臺年利潤為5000萬元；若某臺發電機未運行，則該臺年虧損800萬元，欲使水電站年總利潤的均值達到最大，應安裝發電機多少臺？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
