
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以
),以![]() 為極點,
為極點,![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 且
且![]() .
.
(1)若函數![]() 是奇函數,試證明:對任意的
是奇函數,試證明:對任意的![]() ,恒有
,恒有![]() ;
;
(2)若對于![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值是3,試求實數
上的最大值是3,試求實數![]() 的值;
的值;
(3)設![]() 且
且![]() ,問:是否存在實數
,問:是否存在實數![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() ?如果存在,請求出
?如果存在,請求出![]() 的取值范圍;如果不存在,請說明理由.
的取值范圍;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市疾控中心流感監測結果顯示,自![]() 年
年![]() 月起,該市流感活動一度出現上升趨勢,尤其是
月起,該市流感活動一度出現上升趨勢,尤其是![]() 月以來,呈現快速增長態勢,截止目前流感病毒活動度仍處于較高水平,為了預防感冒快速擴散,某校醫務室采取積極方式,對感染者進行短暫隔離直到康復.假設某班級已知
月以來,呈現快速增長態勢,截止目前流感病毒活動度仍處于較高水平,為了預防感冒快速擴散,某校醫務室采取積極方式,對感染者進行短暫隔離直到康復.假設某班級已知![]() 位同學中有
位同學中有![]() 位同學被感染,需要通過化驗血液來確定感染的同學,血液化驗結果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學為止;
位同學被感染,需要通過化驗血液來確定感染的同學,血液化驗結果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學為止;
方案乙:先任取![]() 個同學,將它們的血液混在一起化驗,若結果呈陽性則表明感染同學為這
個同學,將它們的血液混在一起化驗,若結果呈陽性則表明感染同學為這![]() 位中的
位中的![]() 位,后再逐個化驗,直到能確定感染同學為止;若結果呈陰性則在另外
位,后再逐個化驗,直到能確定感染同學為止;若結果呈陰性則在另外![]() 位同學中逐個檢測;
位同學中逐個檢測;
(1)求依方案甲所需化驗次數等于方案乙所需化驗次數的概率;
(2)![]() 表示依方案甲所需化驗次數,
表示依方案甲所需化驗次數,![]() 表示依方案乙所需化驗次數,假設每次化驗的費用都相同,請從經濟角度考慮那種化驗方案最佳.
表示依方案乙所需化驗次數,假設每次化驗的費用都相同,請從經濟角度考慮那種化驗方案最佳.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V-ABC中,平面VAB⊥平面ABC,△VAB為等邊三角形,AC⊥BC且AC=BC,O,M分別為AB,VA的中點.

(1)求證:VB∥平面MOC;
(2)求證:平面MOC⊥平面VAB;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正方形![]() 中,點
中,點![]() ,
,![]() 分別為邊
分別為邊![]() ,
,![]() 的中點,將
的中點,將![]() 沿
沿![]() 所在直線進行翻折,將
所在直線進行翻折,將![]() 沿
沿![]() 所在直線進行翻折,在翻折的過程中,
所在直線進行翻折,在翻折的過程中,
①點![]() 與點
與點![]() 在某一位置可能重合;②點
在某一位置可能重合;②點![]() 與點
與點![]() 的最大距離為
的最大距離為![]() ;
;
③直線![]() 與直線
與直線![]() 可能垂直; ④直線
可能垂直; ④直線![]() 與直線
與直線![]() 可能垂直.
可能垂直.
以上說法正確的個數為( )
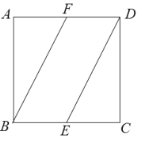
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象所有點向右平移
的圖象所有點向右平移![]() 個單位,再縱坐標不變,橫坐標擴大到原來的
個單位,再縱坐標不變,橫坐標擴大到原來的![]() 倍,得到函數
倍,得到函數![]() 的圖象.
的圖象.
(1)求![]() 的解析式;
的解析式;
(2)在區間![]() 上
上![]() 是否存在的對稱軸?若存在,求出,若不存在說明理由?
是否存在的對稱軸?若存在,求出,若不存在說明理由?
(3)令![]() ,若
,若![]() 滿足
滿足![]() ,且
,且![]() 的終邊不共線,求
的終邊不共線,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個口袋中裝有n個紅球(n≥1且n∈N+)和2個白球,從中有放回地連續摸三次,每次摸出2個球,若2個球顏色不同則為中獎,否則不中獎.
(1)當n=3時,設三次摸球中中獎的次數為X,求隨機變量X的分布列;
(2)記三次摸球中恰有兩次中獎的概率為P,求當n取多少時,P的值最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com