
| A. | 10 | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{13}{2}$ |
分析 根據拋物線的定義,結合|AF|=5,求出A的坐標,然后求出AF的方程求出B點的橫坐標即可得到結論.
解答  解:拋物線的焦點F(1,0),準線方程為x=-1,
解:拋物線的焦點F(1,0),準線方程為x=-1,
設A(x,y),
則|AF|=x+1=5,故x=4,此時y=4,即A(4,4),
則直線AF的方程為$\frac{y-0}{4-0}=\frac{x-1}{4-1}$,即y=$\frac{4}{3}$(x-1),
代入y2=4x得4x2-17x+4=0,
解得x=4(舍)或x=$\frac{1}{4}$,
則|BF|=$\frac{1}{4}$+1=$\frac{5}{4}$,則弦AB的長為:$\frac{25}{4}$.
故選:B.
點評 本題主要考查拋物線的弦長的計算,根據拋物線的定義是解決本題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
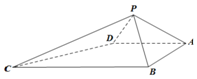 如圖,四棱錐P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等邊三角形,則直線PC與平面ABCD所成角的正切值為( )
如圖,四棱錐P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等邊三角形,則直線PC與平面ABCD所成角的正切值為( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,+∞) | B. | $(\frac{8}{3},+∞)$ | C. | $(\frac{4}{3},+∞)$ | D. | $(\frac{10}{9},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com