
【題目】已知數列{an}的前n項和為Sn,S1=-![]() ,an-4SnSn-1=0(n≥2).
,an-4SnSn-1=0(n≥2).
(1) 若bn=![]() ,求證:{bn}是等差數列;
,求證:{bn}是等差數列;
(2) 求數列{an}的通項公式.
【答案】(1)見解析;(2) .
.
【解析】試題分析:(1)根據an=Sn-Sn-1,結合n≥2時,an-4SnSn-1=0,可得Sn-Sn-1=4SnSn-1,兩邊同除SnSn-1可得結論;
(2)根據(1)可得Sn=-![]() ,結合b1=
,結合b1=![]() =-4,n≥2時,an-4SnSn-1=0,可得數列{an}的通項公式.
=-4,n≥2時,an-4SnSn-1=0,可得數列{an}的通項公式.
試題解析:
(1) 證明:當n≥2時,由an-4SnSn-1=0,an=4SnSn-1,得Sn-Sn-1=4SnSn-1,
所以![]() -
-![]() =-4,即bn-bn-1=-4.
=-4,即bn-bn-1=-4.
又b1=![]() =-4,故{bn}是首項為-4,公差為-4的等差數列.
=-4,故{bn}是首項為-4,公差為-4的等差數列.
(2) 解:由(1)可得bn=-4-4(n-1)=-4n,即![]() =-4n,所以Sn=-
=-4n,所以Sn=-![]() .
.
當n≥2時,an=Sn-Sn-1=-![]() +
+![]() =
=![]() =
=![]() .
.
當n=1時,a1=-![]() 不適合上式.
不適合上式.
故 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某市居民自來水收費標準如下:每戶每月用水不超過5噸時,每噸為![]() 元,當用水超過5噸時,超過部分每噸4元。某月甲、乙兩戶共交水費
元,當用水超過5噸時,超過部分每噸4元。某月甲、乙兩戶共交水費![]() 元,已知甲、乙兩戶該月用水量分別為
元,已知甲、乙兩戶該月用水量分別為![]() 噸。
噸。
(1)求![]() 關于
關于![]() 的函數。
的函數。
(2)若甲、乙兩戶該月共交水費![]() 元,分別求甲、乙兩戶該月的用水量和水費。
元,分別求甲、乙兩戶該月的用水量和水費。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20 000元,每生產一臺儀器需要增加投入100元,已知總收益滿足函數:R(x)=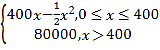 其中x是儀器的月產量.當月產量為何值時,公司所獲得利潤最大?最大利潤是多少?
其中x是儀器的月產量.當月產量為何值時,公司所獲得利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網絡的發展,人們可以在網絡上購物、玩游戲、聊天、導航等,所以人們對上網流量的需求越來越大.某電信運營商推出一款新的“流量包”套餐.為了調查不同年齡的人是否愿意選擇此款“流量包”套餐,隨機抽取50個用戶,按年齡分組進行訪談,統計結果如右表.
組 號 | 年齡 | 訪談 人數 | 愿意 使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4組愿意選擇此款“流量包”套餐的人中,用分層抽樣的方法抽取12人,則各組應分別抽取多少人?
(Ⅱ)若從第5組的被調查者訪談人中隨機選取2人進行追蹤調查,求2人中至少有1人愿意選擇此款“流量包”套餐的概率.
(Ⅲ)按以上統計數據填寫下面2×2列聯表,并判斷以48歲為分界點,能否在犯錯誤不超過1%的前提下認為,是否愿意選擇此款“流量包”套餐與人的年齡有關?
年齡不低于48歲的人數 | 年齡低于48歲的人數 | 合計 | |
愿意使用的人數 | |||
不愿意使用的人數 | |||
合計 |
參考公式:![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水果店購進某種水果的成本為![]() ,經過市場調研發現,這種水果在未來30天的銷售單價
,經過市場調研發現,這種水果在未來30天的銷售單價![]() 與時間
與時間![]() 之間的函數關系式為
之間的函數關系式為![]() ,銷售量
,銷售量![]() 與時間
與時間![]() 的函數關系式為
的函數關系式為![]() 。
。
(Ⅰ)該水果店哪一天的銷售利潤最大?最大利潤是多少?
(Ⅱ)為響應政府“精準扶貧”號召,該店決定每銷售![]() 水果就捐贈
水果就捐贈![]() 元給“精準扶貧”對象.欲使捐贈后不虧損,且利潤隨時間
元給“精準扶貧”對象.欲使捐贈后不虧損,且利潤隨時間![]()
![]() 的增大而增大,求捐贈額
的增大而增大,求捐贈額![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() .
.
(1)如果函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(2)在(1)的條件下,求函數![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(3)已知不等式![]()
![]() 恒成立,若方程
恒成立,若方程![]() 恰有兩個不等實根,求
恰有兩個不等實根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為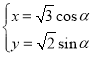 (
(![]() 為參數).
為參數).
(1)已知在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,點
軸正半軸為極軸)中,點![]() 的極坐標為
的極坐標為![]() ,判斷點
,判斷點![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某射擊運動員每次擊中目標的概率都是0.8.現采用隨機模擬的方法估計該運動員射擊4次,至多擊中1次的概率:先由計算器產生0到9之間取整數值的隨機數,指定0,1表示沒有擊中目標,2,3,4,5,6,7,8,9表示擊中目標;因為射擊4次,故以每4個隨機數為一組,代表射擊4次的結果.經隨機模擬產生了20組隨機數:
5 727 0 293 7 140 9 857 0 347
4 373 8 636 9 647 1 417 4 698
0 371 6 233 2 616 8 045 6 011
3 661 9 597 7 424 6 710 4 281
據此估計,該射擊運動員射擊4次至多擊中1次的概率為( )
A. 0.95 B. 0.1
C. 0.15 D. 0.05
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com