【題目】設函數
．
（1）當
時，求
的極值；
（2）如果
≥
在
上恒成立，求實數
的取值范圍．
【答案】
有極小值
，沒有極大值；（2）
．
【解析】試題分析：（1）當
時，求導令導函數等于零，列表，通過表格找到函數極值即可；（2）求恒成立問題一般要分離參數，構造函數求其最小值，只需最小值大于零即可求出
取值范圍.
試題解析：（1）由已知，當
時， 
，∴
， 
∴
在
上單調遞增，且
，
， 
隨
變化如下表：
|
| 1 |
|
| - | 0 | + |
| ↘ | 極小值 | ↗ |
∴
有極小值
，沒有極大值．
（2）（方法一）由題可得
恒成立，
當
時，上式恒成立；
當
時， 
，又
，故
令
，則
， 令
， 
∴當
時， 
， 
時， 
，
∴
，
∴
，解得： 
，∴
的取值范圍是
．
（方法二）由題可得， 設
，則
，
∵
，∴
在
上單調遞增， 
， 
，
∴
使得
，則
，
由
知
，且
時， 
， 
時， 
，
∴
，∴
，∴
，∴
，
∴
的取值范圍是
．
（方法三）由題可得
恒成立，
令
，則
，
∴
時， 
， 
時， 
，∴
，
∴
，解得： 
，∴
的取值范圍是
．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知函數 
．
（1）請在直角坐標系中畫出函數f（x）的圖象，并寫出該函數的單調區間；
（2）若函數g（x）=f（x）﹣m恰有3個不同零點，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司租地建倉庫，每月土地占用費y1與車庫到車站的距離x成反比，而每月的庫存貨物的運費y2與車庫到車站的距離x成正比．如果在距離車站10公里處建立倉庫，這兩項費用y1和y2分別為2萬元和8萬元．求若要使得這兩項費用之和最小時，倉庫應建在距離車站多遠處？此時最少費用為多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從高一年級學生中隨機抽取部分學生，將他們的模塊測試成績分為6組：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以統計，得到如圖所示的頻率分布直方圖，已知高一年級共有學生600名，據此估計，該模塊測試成績不少于60分的學生人數為 ．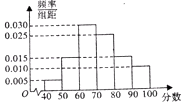 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某環保節能設備生產企業的產品供不應求，已知某種設備的月產量x（套）與每套的售價y1（萬元）之間滿足關系式y1=150﹣ 
x，每套的售價不低于90萬元；月產量x（套）與生產總成本y2（萬元）之間滿足關系式y2=600+72x，則月生產多少套時，每套設備的平均利潤最大？最大平均利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
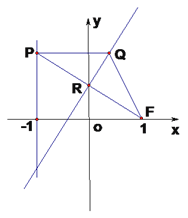
【題目】在平面直角坐標系
中，設點
(1，0)，直線
: 
，點
在直線
上移動， 
是線段
與
軸的交點, 異于點R的點Q滿足： 
， 
.
（1）求動點
的軌跡的方程；
（2） 記
的軌跡的方程為
，過點
作兩條互相垂直的曲線
的弦
. 
，設
. 
的中點分別為
．
問直線
是否經過某個定點？如果是，求出該定點，
如果不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l1：2ax+y﹣1=0，l2：ax+（a﹣1）y+1=0，
（1）若l1⊥l2 ， 求實數a的值；
（2）若l1∥l2時，求直線l1與l2之間的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
，（其中
， 
為自然對數的底數， 
……）.
（1）令
，若
對任意的
恒成立，求實數
的值；
（2）在（1）的條件下，設
為整數，且對于任意正整數
， 
，求
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
