
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC,E是PC的中點(diǎn),作EF⊥PB交PB于點(diǎn)F.
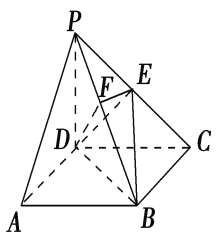
(1)求證:PA∥平面EDB;
(2)求證:PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
【答案】(1)詳見(jiàn)解析(2)詳見(jiàn)解析(3) 60°
【解析】
試題分析:(1)連接AC,AC交BD于O,連接EO要證明PA∥平面EDB,只需證明直線(xiàn)PA平行平面EDB內(nèi)的直線(xiàn)EO;(2)要證明PB⊥平面EFD,只需證明PB垂直平面EFD內(nèi)的兩條相交直線(xiàn)DE、EF,即可;(3)必須說(shuō)明∠EFD是二面角C-PB-D的平面角,然后求二面角C-PB-D的大小
試題解析:(1)證明: 如圖所示,連接AC,AC交BD于O,連接EO.
∵底面ABCD是正方形,
∴點(diǎn)O是AC的中點(diǎn).
在△PAC中,EO是中位線(xiàn),
∴PA∥EO. ……2
而EO平面EDB且PA平面EDB,
∴PA∥平面EDB. ……4
(2)證明: ∵PD⊥底面ABCD,且DC底面ABCD,
∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形.
而DE是斜邊PC的中線(xiàn),∴DE⊥PC.① ……6
同樣,由PD⊥底面ABCD,BC平面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,又PD∩CD=D,
∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②且PC∩BC=C可得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,
∴PB⊥平面EFD. ……8
(3)解 由(2)知,PB⊥DF.
故∠EFD是二面角C-PB-D的平面角. ……9
由(2)知DE⊥EF,PD⊥DB.
設(shè)正方形ABCD的邊長(zhǎng)為a,
則PD=DC=a,BD=![]() a,
a,
PB=![]() a,PC=
a,PC=![]() a,DE=
a,DE=![]() a,
a,
在Rt△PDB中,DF=![]() a.
a.
在Rt△EFD中,sin∠EFD=![]() ,
,
∴∠EFD=60°. ……11
∴二面角C-PB-D的大小為60°. ……12


 學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案
學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 為常數(shù)).
為常數(shù)).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 的兩個(gè)極值點(diǎn)
的兩個(gè)極值點(diǎn)![]() 恰為
恰為![]() 的零點(diǎn),求
的零點(diǎn),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 上的偶函數(shù),其圖象關(guān)于點(diǎn)
上的偶函數(shù),其圖象關(guān)于點(diǎn)![]() 對(duì)稱(chēng),且在區(qū)間
對(duì)稱(chēng),且在區(qū)間![]() 上是單調(diào)函數(shù),則
上是單調(diào)函數(shù),則![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. 無(wú)法確定
D. 無(wú)法確定
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某單位每天的用電量![]() (度)與當(dāng)天最高氣溫
(度)與當(dāng)天最高氣溫![]() (℃)之間具有線(xiàn)性相關(guān)關(guān)系,下表是該單位隨機(jī)統(tǒng)計(jì)4天的用電量與當(dāng)天最高氣溫的數(shù)據(jù).
(℃)之間具有線(xiàn)性相關(guān)關(guān)系,下表是該單位隨機(jī)統(tǒng)計(jì)4天的用電量與當(dāng)天最高氣溫的數(shù)據(jù).
最高氣溫(℃) | 26 | 29 | 31 | 34 |
用電量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根據(jù)表中數(shù)據(jù),求出回歸直線(xiàn)的方程![]() (其中
(其中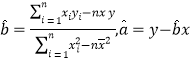 );
);
(Ⅱ)試預(yù)測(cè)某天最高氣溫為33℃時(shí),該單位當(dāng)天的用電量(精確到1度).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在多面體![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
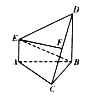
(1)若![]() 是線(xiàn)段
是線(xiàn)段![]() 的中點(diǎn),證明:
的中點(diǎn),證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=sin![]() -2
-2![]() ·sin2x.
·sin2x.
(1) 求函數(shù)f(x)的最小正周期;
(2) 求函數(shù)f(x)圖象的對(duì)稱(chēng)軸方程、對(duì)稱(chēng)中心的坐標(biāo);
(3) 當(dāng)0≤x≤![]() 時(shí),求函數(shù)f(x)的最大、最小值.
時(shí),求函數(shù)f(x)的最大、最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)當(dāng)![]() 時(shí),設(shè)函數(shù)
時(shí),設(shè)函數(shù)![]() .若函數(shù)
.若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有兩個(gè)零點(diǎn),求實(shí)數(shù)
上有兩個(gè)零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() :
:![]()
![]() ;
; ![]() :關(guān)于
:關(guān)于![]() 的方程
的方程![]() 的兩根之差的絕對(duì)值大于3.如果
的兩根之差的絕對(duì)值大于3.如果![]() 為真命題,
為真命題,![]() 為假命題,求實(shí)數(shù)
為假命題,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)開(kāi)發(fā)一種新產(chǎn)品,現(xiàn)準(zhǔn)備投入適當(dāng)?shù)膹V告費(fèi),對(duì)產(chǎn)品進(jìn)行促銷(xiāo),在一年內(nèi),預(yù)計(jì)年銷(xiāo)量Q(萬(wàn)件)與廣告費(fèi)x(萬(wàn)件)之間的函數(shù)關(guān)系為![]() ,已知生產(chǎn)此產(chǎn)品的年固定投入為3萬(wàn)元,每年產(chǎn)1萬(wàn)件此產(chǎn)品仍需要投入32萬(wàn)元,若年銷(xiāo)售額為
,已知生產(chǎn)此產(chǎn)品的年固定投入為3萬(wàn)元,每年產(chǎn)1萬(wàn)件此產(chǎn)品仍需要投入32萬(wàn)元,若年銷(xiāo)售額為![]() ,而當(dāng)年產(chǎn)銷(xiāo)量相等。
,而當(dāng)年產(chǎn)銷(xiāo)量相等。
(1)試將年利潤(rùn)P(萬(wàn)件)表示為年廣告費(fèi)x(萬(wàn)元)的函數(shù);
(2)當(dāng)年廣告費(fèi)投入多少萬(wàn)元時(shí),企業(yè)年利潤(rùn)最大?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com