日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
求極限 (a≠－3)

答案：
解析：

當|a|>3時，，原式；

當|a|<3時，，原式；

當a=3時，原式=0．


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

求下列各極限：
（1）
lim
x→2
（
4
x2-4
-
1
x-2
)；
（2）
lim
x→∞
（
(x+a)(x+b)
-x）；
（3）
lim
x→0
x
|x|
；
（4）
lim
x→
π
2
cosx
cos
x
2
-sin
x
2
.

查看答案和解析>>

科目：高中數學 來源： 題型：

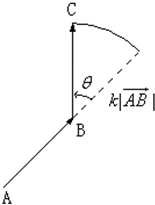精英家教網如圖，
BC
的大小是
AB
大小的k倍，
BC
的方向由
AB
的方向逆時針旋轉θ角得到，則我們稱
AB
經過一次（θ，k）延伸得到
BC
． 已知
OA1
=(1，0)
（1）向量
OA1
經過2次(
π
2
，
1
2
)延伸，分別得到向量
A1A2
、
A2A3
，求
A1A2
、
A2A3
的坐標．
（2）向量
OA1
經過n-1次(
π
2
，
1
2
)延伸得到的最后一個向量
為
An-1An
，（n∈N*，n＞1），設點An（xn，yn），求An的極限位置A(
lim
n→∞
xn，
lim
n→∞
yn)
（3）向量
OA1
經過2次（θ，k）延伸得到向量
A1A2
、
A2A3
，其中k＞0，θ∈（0，π），若
OA1
、
A1A2
、
A2A3
恰能夠構成一個三角形（即A3與O重合），求θ，k的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

求下列各極限:

(1)[++…+];

(2)[n(1-)·(1-)·…·(1-)];

(3)[(1+)·(1+)·(1+)·…·(1+)];

(4)(a≠-3).

查看答案和解析>>

科目：高中數學 來源： 題型：

(理)已知一列非零向量a n,n∈N*,滿足:a1=(10,-5), a n=(xn,yn)=k(xn-1-yn-1,xn-1+yn-1)(n≥2),其中k是非零常數.

(1)求數列{| a n|}的通項公式;

(2)求向量a n-1與a n的夾角(n≥2);

(3)當k=時,把a 1, a 2,…, a n,…中所有與a 1共線的向量按原來的順序排成一列,記為b1,b2,…,bn,…,令OBn=b1+b2+…+bn,O為坐標原點,求點列{Bn}的極限點B的坐標.〔注:若點坐標為(tn,sn),且tn=t,sn=s,則稱點B(t,s)為點列的極限點〕

(文)設函數f(x)=5x-6,g(x)=f(x).

(1)解不等式g(n)［g(1)+g(2)+…+g(n)］＜0(n∈N*);

(2)求h(n)=g(n)［g(1)+g(2)+…+g(n)］-132n(n∈N*)的最小值.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久免费国产 | 午夜影院免费体验区 | 国产一区二区h | 狠狠色丁香九九婷婷综合五月 | 欧美精品在线免费观看 | 久久午夜影院 | 中文字幕亚洲一区二区三区 | 亚洲一区二区三区日韩 | 国产精品高清在线 | 国产精品成人在线 | 国产高清精品一区二区三区 | 国产一区精品视频 | 久久精品一区 | 草久av| 91亚洲一区| 国产精品理论片 | 天天av网 | 国产成人精品综合 | 久久久久久久久国产成人免费 | 亚洲精品乱码久久久久久不卡 | 亚洲啊v | 国产精品一二三区 | 欧美综合国产精品久久丁香 | 亚洲精品日韩激情欧美 | 国产精品二区一区二区aⅴ污介绍 | 亚洲国产一区二区三区 | 久久国产精品久久 | 国产片一区二区 | 久久久av电影 | 久久这里只有精品首页 | 美女久久久久 | 毛片毛片毛片毛片毛片毛片毛片毛片毛片毛片 | 欧美在线网站 | 青青草精品 | 亚洲香蕉精品 | 日韩美一级 | 欧美精品导航 | 亚洲精品一二三四五区 | 欧美色图在线观看 | 精品久久久久久亚洲精品 | 色综合99|