【題目】如圖，在四棱錐
中，
底面
，是邊長為
的正方形．且
，點
是
的中點．
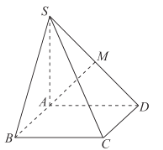
（1）求證：
；
（2）求平面
與平面
所成銳二面角的大小．
【答案】（1）見解析；（2）
.
【解析】
（1）證明出
平面
，由直線與平面垂直的定義可得出
；
（2）解法一：以
、
、
為
、
、
軸建立空間直角坐標系
，由題意得出平面
與平面的一個法向量分別為
、
，然后利用空間向量法計算出平面與平面所成的銳二面角；
解法二：過
引直線
，使得
，可知為平面與平面所成二面角的棱，并證明出
，
，由二面角的定義得出
為平面與平面所成的銳二面角，然后在
計算出該角即可.
（1）由題意，底面
是正方形，
.
底面，
平面，
.
，
平面
.
平面，
.
又
，點
是
的中點，
，
，
平面.
平面，
；
（2）法—：由題知、、兩兩垂直，以、、為、、軸建立空間直角坐標系．
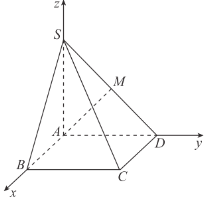
則
，
，則
，
，
平面
，則是平面的一個法向量，
，
由（1）知平面，
是平面的一個法向量，且
，
∴
，
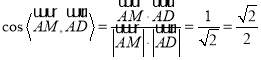因此，平面與平面所成銳二面角的大小等于；
法二：過引直線，使得，則
，
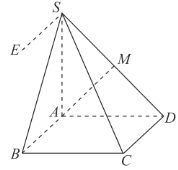
平面，
平面，
就是平面與平面所成二面角的棱．
由條件知，
，
，已知
，則
平面．
由作法知，則
平面，所以，，
就是平面與平面所成銳二面角的平面角．
在
中，
，
平面與平面所成銳二面角的大小等于．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】有一個底面半徑為3，軸截面為正三角形的圓錐紙盒，在該紙盒內放一個棱長均為a的四面體，并且四面體在紙盒內可以任意轉動，則a的最大值為________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，橢圓
的左、右焦點分別為
，
，
為
橢圓上一點，且
垂直于
軸，連結
并延長交橢圓于另一點
，設
.
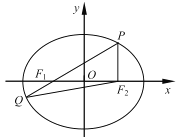
（1）若點的坐標為
，求橢圓的方程及
的值；
（2）若
，求橢圓的離心率的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）若曲線
在
處的切線的斜率為3，求實數
的值；
（2）若函數在區間
上存在極小值，求實數的取值范圍；
（3）如果
的解集中只有一個整數，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在“數學發展史”知識測驗后,甲、乙、丙三人對成績進行預測:
甲說:我的成績比乙高;
乙說:丙的成績比我和甲的都高;
丙說:我的成績比乙高.
成績公布后,三人成績互不相同且只有一個人預測正確,那么三人中預測正確的是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】足球是世界普及率最高的運動，我國大力發展校園足球.為了解本地區足球特色學校的發展狀況，社會調查小組得到如下統計數據：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色學校y（百個） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根據上表數據，計算y與x的相關系數r，并說明y與x的線性相關性強弱.
（已知：
，則認為y與x線性相關性很強；
，則認為y與x線性相關性一般；
，則認為y與x線性相關性較）：
（2）求y關于x的線性回歸方程，并預測A地區2020年足球特色學校的個數（精確到個）.
參考公式和數據：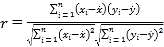
，
，
.
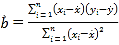
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一個不透明的袋子，裝有4個大小形狀完全相同的小球，球上分別標有數字1，2，3，4.現按如下兩種方式隨機取球兩次，每種方式中第1次取到球的編號記為
，第2次取到球的編號記為
.
（1）若逐個不放回地取球，求
是奇數的概率；
（2）若第1次取完球后將球再放回袋中，然后進行第2次取球，求直線
與雙曲線
有公共點的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
