
(本小題滿分11分)對于定義域為D的函數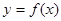 ,如果存在區間
,如果存在區間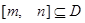 ,同時滿足:
,同時滿足:
①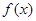 在
在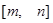 內是單調函數;
內是單調函數;
②當定義域是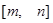 時,
時,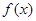 的值域也是
的值域也是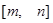 .
.
則稱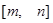 是該函數的“和諧區間”.
是該函數的“和諧區間”.
(1)證明: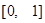 是函數
是函數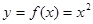 的一個“和諧區間”.
的一個“和諧區間”.
(2)求證:函數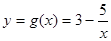 不存在“和諧區間”.
不存在“和諧區間”.
(3)已知函數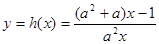 (
(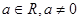 )有“和諧區間”
)有“和諧區間”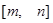 ,當
,當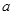 變化時,求出
變化時,求出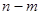 的最大值.
的最大值.
解:(1)區間 是
是 的一個“和諧區間”.
的一個“和諧區間”.
(2)函數 不存在“和諧區間”.
不存在“和諧區間”.
(3)當 時,
時, 取最大值
取最大值 .
.
【解析】本試題主要是結合了函數的單調性和函數的定義域和值域的有關系概念,對于新定義“和諧區間”的理解和靈活的運用。
(1) 在區間
在區間 上單調遞增,并且滿足第二點又
上單調遞增,并且滿足第二點又 ,
, ,
, 值域為
值域為 ,故得到結論。
,故得到結論。
(2)假設存在一個區間滿足題意,利用反比列函數的性質可知,沒有和諧區間。
(3)根據已知條件可知,函數存在和諧區間,那么可以設出區間,再分析函數的單調性,得到定義域和值域的關系,進而得到結論。
解:(1) 在區間
在區間 上單調遞增.
上單調遞增.
又 ,
, ,
, 值域為
值域為 ,
,
 區間
區間 是
是 的一個“和諧區間”.…………2分
的一個“和諧區間”.…………2分
(2)設 是已知函數定義域的子集.
是已知函數定義域的子集. ,
, 或
或 ,故函數
,故函數 在
在 上單調遞增.
上單調遞增.
若 是已知函數的“和諧區間”,則
是已知函數的“和諧區間”,則
故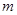 、
、 是方程
是方程 的同號的相異實數根.
的同號的相異實數根.
 無實數根,
無實數根, 函數
函數 不存在“和諧區間”.………………5分
不存在“和諧區間”.………………5分
(3)設 是已知函數定義域的子集.
是已知函數定義域的子集. ,
, 或
或 ,故函數
,故函數 在
在 上單調遞增.
上單調遞增.
若 是已知函數的“和諧區間”,則
是已知函數的“和諧區間”,則
故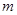 、
、 是方程
是方程 ,即
,即 的同號的相異實數根.
的同號的相異實數根.
 ,
, ,
, 同號,只須
同號,只須 ,即
,即 或
或 時,已知函數有“和諧區間”
時,已知函數有“和諧區間” ,
, ,
,
 當
當 時,
時, 取最大值
取最大值 ………………11分
………………11分


科目:高中數學 來源:2013屆浙江省高二下學期期中文科數學試卷(解析版) 題型:解答題
(本小題滿分11分) 已知函數 ,其中
,其中 .
.
(1) 當 時,求
時,求 的單調區間;
的單調區間;
(2) 證明:對任意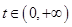 ,
, 在區間
在區間 內存在零點.
內存在零點.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高二上學期期中考試理科數學 題型:解答題
(本小題滿分11分)
已知a、b、c為三角形ABC中角A、B、C的對邊,且
 ,求這個三角形的最大內角.
,求這個三角形的最大內角.
查看答案和解析>>
科目:高中數學 來源:2010年陜西省西安市鐵一中高二下學期期中考試數學(理) 題型:解答題
(本小題滿分11分)已知,
 ;
;
(1)試由此歸納出當 時相應的不等式;
時相應的不等式;
(2)試用數學歸納法證明你在第(1)小題得到的不等式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com